Question

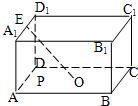例2：如图，在长方体ABCD-A₁B₁C₁D₁中，AB=AD=2AA₁=4，点O是底面ABCD的中心，点E是A₁D₁的中点，点P是底面ABCD上的动点，且到直线OE的距离等于1，对于点P的轨迹，下列说法正确的是（　　）

• A、离心率为

  2

  2

  的椭圆
• B、离心率为

  1

  2

  的椭圆
• C、一段抛物线
• D、半径等于1的圆

Answer 1

分析：由题意可知点P在以OE为轴，半径为1的圆柱侧面上，点P又在底面ABCD上，得点P的轨迹是平面ABCD与圆柱侧面的交线，想象知其必为椭圆，由轴OE与ABCD成45°，可算得其离心率

解答：解：由题意可知：知点P的轨迹为椭圆，作EF⊥AD于点F，则EF=OF=2，△OEF为等腰直角三角形，得轴OE与平面ABCD所成的角为45°，知点P的轨迹是椭圆，而半长轴长a=

2

，短半轴长为b=1，则c²=a²-b²=1，∴e=

1

2

=

2

2

．
故选A．

点评：初看综合性较强，但从“交轨法”的角度考虑问题后，再配合题中所给的数据，也就不难解决了．是个基础题．