题目内容
已知f(x)是周期为2的奇函数,当0<x<1时,f(x)=lgx,设a=f(
),b=f(
),c=f(
),则( )
| A．c<a<b | B．a<b<c | C．b<a<c | D．c<b<a |
A
解析
练习册系列答案
单元期中期末卷系列答案
相关题目
已知函数
，
，则（ ）
A． 与 均为偶函数 | B．为奇函数，为偶函数 |
| C．与均为奇函数 | D．为偶函数,为奇函数 |
下列函数为偶函数的是( )
| A．y=sinx | B．y=x3 |
| C．y=ex | D．y=ln |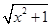
下列函数中，为偶函数且有最小值的是( )
| A．f(x)＝x2＋x | B．f(x)＝|ln x| |
| C．f(x)＝xsin x | D．f(x)＝ex＋e－x |
函数f(x)=
的定义域为( )
| A．(0,+∞) | B．(1,+∞) |
| C．(0,1) | D．(0,1)∪(1,+∞) |
“a≤0”是“函数f(x)＝|(ax－1)x|在区间(0，＋∞)内单调递增”的( )
| A．充分不必要条件 | B．必要不充分条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
设f(x)是连续的偶函数,且当x>0时是单调函数,则满足f(x)=f(
)的所有x之和为( )
| A．-3 | B．3 | C．-8 | D．8 |
若函数y=ax与y=-
在(0,+∞)上都是减函数,则y=ax2+bx在(0,+∞)上是( )
| A．增函数 | B．减函数 | C．先增后减 | D．先减后增 |
函数y＝f(x)的图象如图所示，在区间[a，b]上可找到n(n≥2)个不同的数x1，x2，…，xn，使得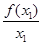
＝
＝…＝
，则n的取值范围为( )．
| A．{3,4} | B．{2,3,4} | C．{3,4,5} | D．{2,3} |