题目内容
“k=5”是“两直线kx+5y-2=0和(4-k)x+y-7=0互相垂直”的
- A.充分不必要条件
- B.必要不充分条件
- C.充要条件
- D.既不充分也不必要条件
A
分析:验证:“k=1”时,两条直线为5x+5y-2=0与-x+y-7=0垂直比较易,对于“?”只须两线斜率乘积为-1即可.
解答:“k=1”时,两条直线为5x+5y-2=0与-x+y-7=0垂直,充分条件成立;
kx+5y-2=0和(4-k)x+y-7=0互相垂直时,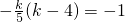 解得k=5或k=-1,必要条件不成立
解得k=5或k=-1,必要条件不成立
所以“k=5”是“两直线kx+5y-2=0和(4-k)x+y-7=0互相垂直”的充分不必要条件.
故选A.
点评:本题主要考查直线与直线垂直的判定,以及充要条件,是基础题目.
分析:验证:“k=1”时,两条直线为5x+5y-2=0与-x+y-7=0垂直比较易,对于“?”只须两线斜率乘积为-1即可.
解答:“k=1”时,两条直线为5x+5y-2=0与-x+y-7=0垂直,充分条件成立;
kx+5y-2=0和(4-k)x+y-7=0互相垂直时,
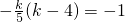 解得k=5或k=-1,必要条件不成立
解得k=5或k=-1,必要条件不成立所以“k=5”是“两直线kx+5y-2=0和(4-k)x+y-7=0互相垂直”的充分不必要条件.
故选A.
点评:本题主要考查直线与直线垂直的判定,以及充要条件,是基础题目.

练习册系列答案
相关题目
已知函数f(x)=
sinwx+coswx(w>0),y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则f(x)的单调递增区间是( )
| 3 |
A、[kπ-
| ||||
B、[kπ+
| ||||
C、[kπ-
| ||||
D、[kπ+
|