题目内容
给出以下命题:
①双曲线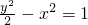 的渐近线方程为
的渐近线方程为 ;
;
②命题p:“?x∈R+,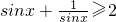 ”是真命题;
”是真命题;
③已知线性回归方程为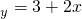 ,当变量x增加2个单位,其预报值平均增加4个单位;
,当变量x增加2个单位,其预报值平均增加4个单位;
④设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=0.2,则P(-1<ξ<0)=0.6;
⑤已知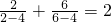 ,
,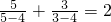 ,
,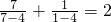 ,
,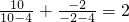 ,依照以上各式的规律,得到一般性的等式为
,依照以上各式的规律,得到一般性的等式为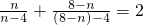 ,(n≠4)
,(n≠4)
则正确命题的序号为________(写出所有正确命题的序号).
①③⑤
分析:①由双曲线渐近线方程的求法可得;②可举反例x= 说明命题错误;③由线性回归方程的意义可得结论;④随机变量ξ服从正态分布N(0,1),由概率和为1可得答案;
说明命题错误;③由线性回归方程的意义可得结论;④随机变量ξ服从正态分布N(0,1),由概率和为1可得答案;
⑤观察已知的式子,由合情推理的知识可得到一般性的结论.
解答:①双曲线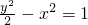 为焦点在y轴的双曲线,且a=
为焦点在y轴的双曲线,且a= ,b=1,
,b=1,
故其渐近线方程为,y=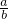 x,即
x,即 ,故正确;
,故正确;
②当x= 时,
时,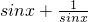 =-2,显然不满足
=-2,显然不满足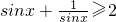 ,
,
故命题p:“?x∈R+,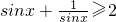 ”应为真命题,故错误;
”应为真命题,故错误;
③由线性回归方程为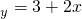 ,可得3+2(x+2)-3-2x=4,
,可得3+2(x+2)-3-2x=4,
即当变量x增加2个单位,其预报值平均增加4个单位,故正确;
④设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=0.2,
则P(-1<ξ<0)=P((0<ξ<1)=0.5-P(ξ>1)=0.5-0.2=0.3,故错误;
⑤已知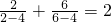 ,
,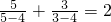 ,
,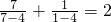 ,
,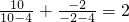 ,
,
由合情推理的知识可得到一般性的等式为: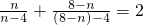 ,(n≠4),故正确.
,(n≠4),故正确.
故答案为:①③⑤
点评:本题考查命题真假的判断与应用,涉及正态分布和合情推理等知识,属基础题.
分析:①由双曲线渐近线方程的求法可得;②可举反例x=
 说明命题错误;③由线性回归方程的意义可得结论;④随机变量ξ服从正态分布N(0,1),由概率和为1可得答案;
说明命题错误;③由线性回归方程的意义可得结论;④随机变量ξ服从正态分布N(0,1),由概率和为1可得答案;⑤观察已知的式子,由合情推理的知识可得到一般性的结论.
解答:①双曲线
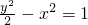 为焦点在y轴的双曲线,且a=
为焦点在y轴的双曲线,且a= ,b=1,
,b=1,故其渐近线方程为,y=
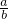 x,即
x,即 ,故正确;
,故正确;②当x=
 时,
时,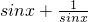 =-2,显然不满足
=-2,显然不满足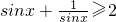 ,
,故命题p:“?x∈R+,
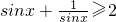 ”应为真命题,故错误;
”应为真命题,故错误;③由线性回归方程为
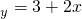 ,可得3+2(x+2)-3-2x=4,
,可得3+2(x+2)-3-2x=4,即当变量x增加2个单位,其预报值平均增加4个单位,故正确;
④设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=0.2,
则P(-1<ξ<0)=P((0<ξ<1)=0.5-P(ξ>1)=0.5-0.2=0.3,故错误;
⑤已知
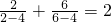 ,
,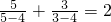 ,
,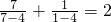 ,
,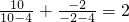 ,
,由合情推理的知识可得到一般性的等式为:
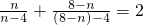 ,(n≠4),故正确.
,(n≠4),故正确.故答案为:①③⑤
点评:本题考查命题真假的判断与应用,涉及正态分布和合情推理等知识,属基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
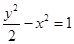 的渐近线方程为
的渐近线方程为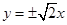 ;
;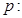 “
“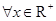 ,
,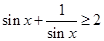 ”是真命题;
”是真命题; ,当变量
,当变量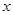 增加
增加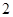 个单位,其预报值平均增加
个单位,其预报值平均增加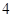 个单位;
个单位;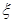 服从正态分布
服从正态分布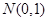 ,若
,若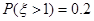 ,则
,则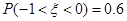 ;
;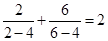 ,
,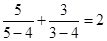 ,
,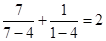 ,
,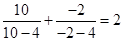 ,依照以上各式的规律,得到一般性的等式为
,依照以上各式的规律,得到一般性的等式为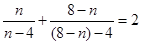 ,(
,(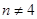 )
) 的渐近线方程为
的渐近线方程为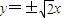 ;
;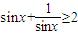 ”是真命题;
”是真命题;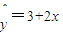 ,当变量x增加2个单位,其预报值平均增加4个单位;
,当变量x增加2个单位,其预报值平均增加4个单位;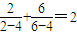 ,
,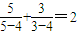 ,
,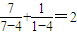 ,
,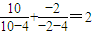 ,依照以上各式的规律,得到一般性的等式为
,依照以上各式的规律,得到一般性的等式为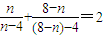 ,(n≠4)
,(n≠4)