题目内容
如果空间三条直线a，b，c两两成异面直线，那么与a，b，c都相交的直线有（ ）
分析：在a、b、c上取三条线段AB、CC′、A′D′，作一个平行六面体ABCD-A′B′C′D′，如图所示．由直线c上一点P与直线a确定的平面β，β和直线b交于点R，由面面平行的性质和平行线的性质得到PR与与直线a是相交直线，故直线PR是与a，b，c都相交的一条直线．最后根据点P的任意性，可得满足条件的直线有无数多条．
解答：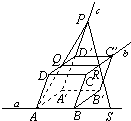
解：在a、b、c上取三条线段AB、CC′、A′D′，
作一个平行六面体ABCD-A′B′C′D′，如右图所示
在c上，即在直线A′D′上取一点P，过a、P作一个平面β
平面β与DD′交于Q、与CC′交于R，则
由面面平行的性质定理，得QR∥a，
于是PR不与a平行，但PR与a共面．故PR与a相交，得直线PR是与a，b，c都相交的一条直线．
根据点P的任意性，得与a，b，c都相交的直线有无穷多条．
故选：D
解：在a、b、c上取三条线段AB、CC′、A′D′，作一个平行六面体ABCD-A′B′C′D′，如右图所示
在c上，即在直线A′D′上取一点P，过a、P作一个平面β
平面β与DD′交于Q、与CC′交于R，则
由面面平行的性质定理，得QR∥a，
于是PR不与a平行，但PR与a共面．故PR与a相交，得直线PR是与a，b，c都相交的一条直线．
根据点P的任意性，得与a，b，c都相交的直线有无穷多条．
故选：D
点评：本题给出空间两两异面的三条直线，求与它们都相交的直线的条数，着重考查了空间直线的位置关系和线面平行的性质等知识，属于中档题．
练习册系列答案
考前必练系列答案
相关题目