题目内容
若平行四边形的3个顶点分别是(4,2),(5,7),( 3,4),则第4个顶点的坐标不可能是( )
3,4),则第4个顶点的坐标不可能是( )
| A.(12,5) | B.(-2,9) | C.(3,7) | D.(-4,-1) |
C
解析试题分析:设第4个顶点坐标为D(m,n),记A(4,2),B(5,7),C(-3,4),∵四边形ABCD为平行四边形,∴ 或
或 或
或 ,∴
,∴ 或
或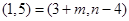 或
或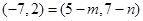 ,∴点D为(-4,-1)或(-2,9)或(12,5),故第4个点坐标不可能为(3,7),故选C
,∴点D为(-4,-1)或(-2,9)或(12,5),故第4个点坐标不可能为(3,7),故选C
考点:本题考查了向量相等的概念
点评:平行四边形的性质,建立平面直角坐标系,数形结合,分类讨论是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
△ABC中,若 ,
, ,则
,则 =( )
=( )
A. | B. | C. | D. |
设O是正△ABC的中心,则向量 ,
, ,
, 是( )
是( )
| A.相等向量 | B.模相等的向量 |
| C.共线向量 | D.共起点的向量 |
若两个非零向量 满足
满足 ,则向量
,则向量 与
与 的夹角为( )
的夹角为( )
A. | B. | C. | D. |
如图,网格纸上小正方形的边长为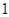 ,粗线画出的是某几何体的
,粗线画出的是某几何体的
三视图,则此几何体的体积为( )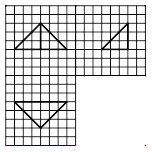
A.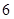 | B.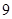 | C. | D.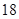 |
已知 ,则与
,则与 共线的向量为
共线的向量为
A. | B. | C.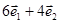 | D. |
在平行四边形ABCD中,  +
+  +
+ 等于( )
等于( )
A. | B. | C.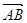 | D. |
正方形ABCD内有一个正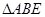 ,设
,设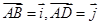 ,则
,则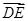 等于
等于
A.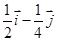 | B.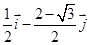 | C.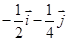 | D.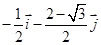 |
已知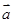 =(2,3),
=(2,3),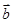 =(4,x),且
=(4,x),且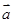 ∥
∥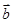 ,则x的值为( )
,则x的值为( )
| A.6 | B.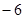 | C.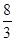 | D.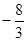 |