题目内容
已知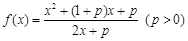
(1)若p >1时,解关于x的不等式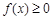 ;
;
(2)若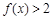 对
对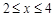 时恒成立,求p的范围.
时恒成立,求p的范围.
(1) ①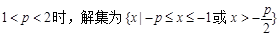 ,
,
② p = 2时,解集为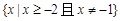 ,
,
③ p > 2时,解集为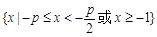 ;
;
(2) p > 2
解析试题分析:(1)先因式分解把原不等式转化为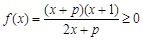 .再对三个根的大小进行讨论求解.
.再对三个根的大小进行讨论求解.
(2)解本小题的关键是把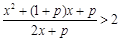 ,
,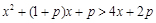 ,
,
∴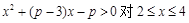 恒成立,最终转化为
恒成立,最终转化为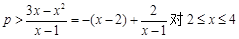 恒成立来解决,然后再构造函数求最值即可.
恒成立来解决,然后再构造函数求最值即可.
(1) 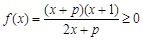 ·························· 1分
·························· 1分
①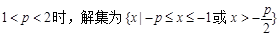 ················· 3分
················· 3分
② p = 2时,解集为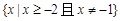 ····················· 5分
····················· 5分
③ p > 2时,解集为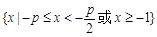 ·················· 7分
·················· 7分
(2) 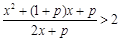
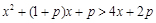 ··························· 8分
··························· 8分
∴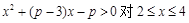 恒成立
恒成立
∴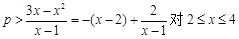 恒成立················· 9分
恒成立················· 9分
∵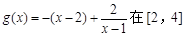 上递减···················· 10分
上递减···················· 10分
∴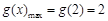 ····························· 11分
····························· 11分
∴ p > 2 12分
考点:解式不等式的解法,不等式恒成立,函数的最值.
点评:(1)分式不等式求解时一般要用数轴穿根法求解.(2)不等式恒成立问题一般要注意参数与变量分离,然后转化为函数最值来研究.

练习册系列答案
相关题目
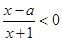 的解集为P,不等式
的解集为P,不等式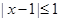 的解集为Q.
的解集为Q.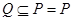 求正数a的取值范围
求正数a的取值范围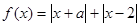
 的解集
的解集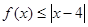 的解集包含[1,2],求
的解集包含[1,2],求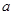 的取值范围
的取值范围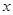 的不等式
的不等式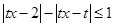 ,其中
,其中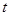 是实参数.
是实参数.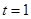 时,解上面的不等式.
时,解上面的不等式.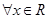 ,上面的不等式均成立,求实数
,上面的不等式均成立,求实数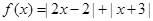 .
.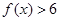 ;
; 的不等式
的不等式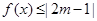 的解集不是空集,试求实数
的解集不是空集,试求实数 的取值范围.
的取值范围.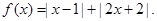
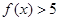 ;
;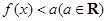 的解集为空集,求
的解集为空集,求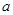 的取值范围.
的取值范围.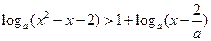 (a>0,a≠1).
(a>0,a≠1).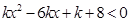 的解集为空集,求实数k的取值范围.
的解集为空集,求实数k的取值范围.