题目内容
过点(-5,-4)作一直线l,使它与两坐标轴相交且与两轴所围成的三角形面积为5个平方单位,求直线l的方程.
思路分析:直线l应满足的两个条件是:(1)直线l过定点(-5,-4);(2)直线l与两坐标轴相交且与两轴所围成的三角形面积是5个平方单位.如果用a、b分别表示l在x轴、y轴上的截距,条件(2)即为![]() |a|·|b|=5,这样就有如下两种不同的解题思路.第一,利用条件(2)设出直线l的方程(截距式),结合条件(1)确定a、b的值;第二,利用条件(1)设出直线l的方程(点斜式),利用条件(2)确定k的值.
|a|·|b|=5,这样就有如下两种不同的解题思路.第一,利用条件(2)设出直线l的方程(截距式),结合条件(1)确定a、b的值;第二,利用条件(1)设出直线l的方程(点斜式),利用条件(2)确定k的值.
解法一:设直线l的方程是![]() +
+![]() =1.
=1.
∵直线l经过点(-5,-4),
∴![]() =1.∵
=1.∵![]() |a|·|b|=5,
|a|·|b|=5,
∴ab=±10.解得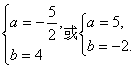
∴所求直线l的方程是8x-5y+20=0或2x-5y-10=0.
解法二:设直线l的方程是y+4=k(x+5),
分别令y=0,x=0,得l在x轴、y轴上的截距是a=![]() ,b=5k-4.
,b=5k-4.
由已知,得ab=±10,
∴![]() ·(5k-4)=±10,
·(5k-4)=±10,
即25k2-30k+16=0或25k2-50k+16=0.∴k=![]() 或k=
或k=![]() .
.
∴所求直线l的方程是8x-5y+20=0或2x-5y-10=0.

练习册系列答案
相关题目
 给定椭圆C:
给定椭圆C: 的切线,其方程是( )
的切线,其方程是( )