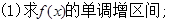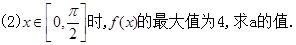题目内容
已知函数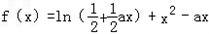 .(a为常数,a>0)
.(a为常数,a>0)
(Ⅰ)若 是函数f(x)的一个极值点,求a的值;
是函数f(x)的一个极值点,求a的值;
(Ⅱ)求证:当0<a≤2时,f(x)在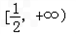 上是增函数;
上是增函数;
(Ⅲ)若对任意的a∈(1,2),总存在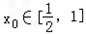 ,使不等式f(x0)>m(1﹣a2)成立,求实数m的取值范围.
,使不等式f(x0)>m(1﹣a2)成立,求实数m的取值范围.
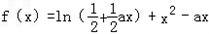 .(a为常数,a>0)
.(a为常数,a>0)(Ⅰ)若
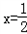 是函数f(x)的一个极值点,求a的值;
是函数f(x)的一个极值点,求a的值;(Ⅱ)求证:当0<a≤2时,f(x)在
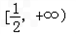 上是增函数;
上是增函数;(Ⅲ)若对任意的a∈(1,2),总存在
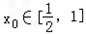 ,使不等式f(x0)>m(1﹣a2)成立,求实数m的取值范围.
,使不等式f(x0)>m(1﹣a2)成立,求实数m的取值范围.解:由题得: .
.
(Ⅰ)由已知,得 且
且 ,
,
∴a2﹣a﹣2=0,
∵a>0,∴a=2.
(Ⅱ)当0<a≤2时,
∵ ,
,
∴ ,
,
∴当 时,
时, .
.
又 ,∴f'(x)≥0,故f(x)在
,∴f'(x)≥0,故f(x)在 上是增函数.
上是增函数.
(Ⅲ)a∈(1,2)时,由(Ⅱ)知,
f(x)在 上的最大值为
上的最大值为 ,
,
于是问题等价于:对任意的a∈(1,2),不等式 恒成立.
恒成立.
记 ,(1<a<2)
,(1<a<2)
则 ,
,
当m=0时, ,
,
∴g(a)在区间(1,2)上递减,此时,g(a)<g(1)=0,由于a2﹣1>0,
∴m≤0时不可能使g(a)>0恒成立,故必有m>0,
∴ .
.
若 ,可知g(a)在区间
,可知g(a)在区间 上递减,在此区间上,有
上递减,在此区间上,有
g(a)<g(1)=0,与g(a)>0恒成立矛盾,故 ,
,
这时,g'(a)>0,g(a)在(1,2)上递增,恒有g(a)>g(1)=0,满足题设要求,
∴ ,即
,即 ,
,
,实数m的取值范围为 .
.
 .
.(Ⅰ)由已知,得
 且
且 ,
,∴a2﹣a﹣2=0,
∵a>0,∴a=2.
(Ⅱ)当0<a≤2时,
∵
 ,
,∴
 ,
,∴当
 时,
时, .
.又
 ,∴f'(x)≥0,故f(x)在
,∴f'(x)≥0,故f(x)在 上是增函数.
上是增函数.(Ⅲ)a∈(1,2)时,由(Ⅱ)知,
f(x)在
 上的最大值为
上的最大值为 ,
,于是问题等价于:对任意的a∈(1,2),不等式
 恒成立.
恒成立.记
 ,(1<a<2)
,(1<a<2)则
 ,
,当m=0时,
 ,
,∴g(a)在区间(1,2)上递减,此时,g(a)<g(1)=0,由于a2﹣1>0,
∴m≤0时不可能使g(a)>0恒成立,故必有m>0,
∴
 .
.若
 ,可知g(a)在区间
,可知g(a)在区间 上递减,在此区间上,有
上递减,在此区间上,有g(a)<g(1)=0,与g(a)>0恒成立矛盾,故
 ,
,这时,g'(a)>0,g(a)在(1,2)上递增,恒有g(a)>g(1)=0,满足题设要求,
∴
 ,即
,即 ,
,,实数m的取值范围为
 .
.
练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 的单调区间.
的单调区间. ,其中a为常数.则“
,其中a为常数.则“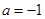 ”是f(x)为奇函数”的
”是f(x)为奇函数”的 (其中a为常数)
(其中a为常数)