题目内容
对一切正整数n,不等式 恒成立,则实数x的取值范围是 .
恒成立,则实数x的取值范围是 .
【答案】分析:把不等式等价转化为x> +
+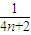 恒成立,由于
恒成立,由于 +
+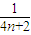 是个单调减函数,n=1时,
是个单调减函数,n=1时, +
+ 有最大值为
有最大值为 ,故得实数x的取值范围.
,故得实数x的取值范围.
解答:解:由题意知,实数x应是正数,不等式即 2- >
>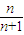 恒成立,即
恒成立,即 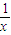 <
<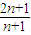 恒成立,
恒成立,
即x>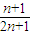 =
= +
+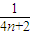 恒成立,
恒成立,
∵ +
+ 是个单调减函数,∴正整数n=1时,
是个单调减函数,∴正整数n=1时, +
+ 有最大值为
有最大值为 ,
,
∴实数x的取值范围是( ,+∞),
,+∞),
故答案为 ( ,+∞).
,+∞).
点评:本题考查绝对值不等式的解法(关键是去掉绝对值),以及函数的恒成立问题,利用单调性求函数的最值.
 +
+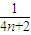 恒成立,由于
恒成立,由于 +
+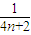 是个单调减函数,n=1时,
是个单调减函数,n=1时, +
+ 有最大值为
有最大值为 ,故得实数x的取值范围.
,故得实数x的取值范围.解答:解:由题意知,实数x应是正数,不等式即 2-
 >
>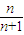 恒成立,即
恒成立,即 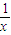 <
<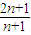 恒成立,
恒成立,即x>
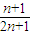 =
= +
+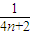 恒成立,
恒成立,∵
 +
+ 是个单调减函数,∴正整数n=1时,
是个单调减函数,∴正整数n=1时, +
+ 有最大值为
有最大值为 ,
,∴实数x的取值范围是(
 ,+∞),
,+∞),故答案为 (
 ,+∞).
,+∞).点评:本题考查绝对值不等式的解法(关键是去掉绝对值),以及函数的恒成立问题,利用单调性求函数的最值.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 恒成立,则实数x的取值范围是
▲ .
恒成立,则实数x的取值范围是
▲ .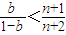 恒成立,则b的范围是( )
恒成立,则b的范围是( )
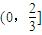
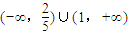

 恒成立,则实数x的取值范围是 .
恒成立,则实数x的取值范围是 .