题目内容
已知A、B分别是x轴和y轴上的两个动点,满足|AB|=2,点P在线段AB上,且
=t
(t是不为0的常数),设点P的轨迹方程为C.
(Ⅰ)求点P的轨迹方程C;
(Ⅱ)若曲线C为焦点在x轴上的椭圆,试求实数t的取值范围;
(Ⅲ)若t=2,点M、N是C上关于原点对称的两个动点,点Q的坐标为(
,3),求△QMN的面积S的最大值.
| AP |
| PB |
(Ⅰ)求点P的轨迹方程C;
(Ⅱ)若曲线C为焦点在x轴上的椭圆,试求实数t的取值范围;
(Ⅲ)若t=2,点M、N是C上关于原点对称的两个动点,点Q的坐标为(
| 3 |
| 2 |
(Ⅰ)设点A(a,0),B(0,b),C(x,y),
∵
=t
,即(x-a,y)=t(-x,b-y),即
(2分)
则
.
又∵|AB|=2,即a2+b2=4.
∴
+
=1.
∴点P的轨迹方程C:
+
=1.(5分)
(Ⅱ)∵曲线C为焦点在x轴上的椭圆,
∴
>
,得t2<1.
又∵t>0,∴0<t<1.(8分)
(Ⅲ)当t=2时,曲线C的方程为
+
=1.(9分)
设M(x1,y1),N(-x1,-y1),则|MN|=2
.
当x1≠0时,设直线MN的方程为y=
x,
则点Q到直线MN的距离h=
,
∴△QMN的面积S=
•2
•
=|
y1-3x1|.(11分)
∴S2=|
y1-3x1|2=9x12+
y12-9x1y1.
又∵
+
=1,
∴9x12+
y12=4.
∴S2=4-9x1y1.
而1=
+
≥-2•
•
=-
,
则-9x1y1≤4.即S2≤8,S≤2
.
当且仅当
=-
时,
即x1=-
y1时,“=”成立.
当x1=0时,|MN|=2•
=
,
∴△QMN的面积S=
•
•
=2.
∴S有最大值2
.(14分)
∵
| AP |
| PB |
|
则
|
又∵|AB|=2,即a2+b2=4.
∴
| (1+t)2x2 |
| 4 |
| (1+t)2y2 |
| 4t2 |
∴点P的轨迹方程C:
| x2 | ||
|
| y2 | ||
|
(Ⅱ)∵曲线C为焦点在x轴上的椭圆,
∴
| 4 |
| (1+t)2 |
| 4t2 |
| (1+t)2 |
又∵t>0,∴0<t<1.(8分)
(Ⅲ)当t=2时,曲线C的方程为
| 9x2 |
| 4 |
| 9y2 |
| 16 |
设M(x1,y1),N(-x1,-y1),则|MN|=2
| x12+y12 |
当x1≠0时,设直线MN的方程为y=
| y1 |
| x1 |
则点Q到直线MN的距离h=
|
| ||
|
∴△QMN的面积S=
| 1 |
| 2 |
| x12+y12 |
|
| ||
|
| 3 |
| 2 |
∴S2=|
| 3 |
| 2 |
| 9 |
| 4 |
又∵
| 9x12 |
| 4 |
| 9y12 |
| 16 |
∴9x12+
| 9 |
| 4 |
∴S2=4-9x1y1.
而1=
| 9x12 |
| 4 |
| 9y12 |
| 16 |
| 3x1 |
| 2 |
| 3y1 |
| 4 |
| 9x1y1 |
| 4 |
则-9x1y1≤4.即S2≤8,S≤2
| 2 |
当且仅当
| 3x1 |
| 2 |
| 3y1 |
| 4 |
即x1=-
| 1 |
| 2 |
当x1=0时,|MN|=2•
| 4 |
| 3 |
| 8 |
| 3 |
∴△QMN的面积S=
| 1 |
| 2 |
| 8 |
| 3 |
| 3 |
| 2 |
∴S有最大值2
| 2 |

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 ,设点P的轨迹方程为C.
,设点P的轨迹方程为C.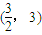 ,求△QMN的面积S的最大值.
,求△QMN的面积S的最大值.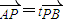 (t是不为0的常数),设点P的轨迹方程为C.
(t是不为0的常数),设点P的轨迹方程为C.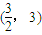 ,求△QMN的面积S的最大值.
,求△QMN的面积S的最大值.