题目内容
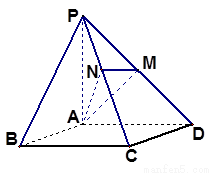
如图,已知四棱锥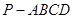 ,底面
,底面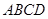 为菱形,
为菱形,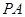
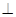 平面
平面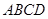 ,
,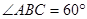 ,
,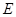 、
、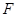 分别是
分别是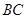 、
、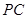 的中点。
的中点。
(1)证明: ;
;
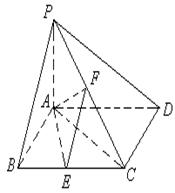 (2)若
(2)若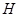 为
为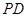 上的动点,
上的动点,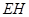 与平面
与平面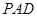 所成最大角的正切值为
所成最大角的正切值为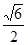 ,求锐二面角
,求锐二面角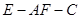 的余弦值;
的余弦值;
(3)在(2)的条件下,设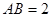 ,求点
,求点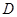 到平面
到平面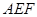 的距离。
的距离。
略
【解析】(1)证明:由四边形 为菱形,
为菱形, ,知
,知 为正三角形
为正三角形
∵ 为
为 的中点 ∴
的中点 ∴ ,又
,又 ∴
∴ …………………………1分
…………………………1分
∵ 平面
平面 ,
, 平面
平面 ∴
∴
而 平面
平面 ,
, 平面
平面 ,且
,且 ,
,
∴ 平面
平面 ,又
,又 平面
平面 ,∴
,∴ …………………………3分
…………………………3分
(2)设 ,连结
,连结
由(1)知 平面
平面 ,而
,而 ,∴
,∴ ,
,
则 为
为 与平面
与平面 所成的角。………………………………………………
4分[来源:ZXXK]
所成的角。………………………………………………
4分[来源:ZXXK]
在 中,
中, ,当
,当 最小时,即当
最小时,即当 时,
时, 最大,此时
最大,此时
 因此
因此 ,
,
又 ∴
∴ ∴
∴ …………………………………………………
5分
…………………………………………………
5分
方法一: 平面
平面 ,
, 平面
平面 , ∴平面
, ∴平面 平面
平面
过 作
作 于
于 ,则
,则 平面
平面 ,过
,过 作
作 于
于 ,连结
,连结 ,则
,则 为二面角
为二面角 的平面角。…………………………………………………… 6分
的平面角。…………………………………………………… 6分
在 中,
中,
 又
又 为的中点,∴
为的中点,∴ 在
在 中,
中, ,
,
又
在 中,
中,
即所求二面角的余弦值为 ……………………………………………………………7分
……………………………………………………………7分
方法二:由(1)知两两垂直,以为坐标原点,建立如图所示的空间直角坐标系,则:

 ∴
∴ ………………………………………………………7分
………………………………………………………7分
设平面 的一个法向量为
的一个法向量为 ,
,
则 ,因此
,因此
取 ,则
,则 ……………………………………………………………
8分
……………………………………………………………
8分
∵ ,
, 平面
平面
故 为平面的法向量。……………………………………………………6分
为平面的法向量。……………………………………………………6分
∴
二面角为锐角,所以所求二面角的余弦值为 …………………………………………
7分
…………………………………………
7分
(3)方法一:由(2)得:在 中,
中, ,∴
,∴
在 中,
中, ,∴
,∴ 中,
中, ,[来源:Z&xx&k.Com]
,[来源:Z&xx&k.Com]
又 ,∴
,∴ ………………………………………………………………
8分
………………………………………………………………
8分
又 ,点
,点 到平面
到平面 的距离
的距离 ,………………… 9分
,………………… 9分
设点 到平面
到平面 的距离为
的距离为 ,
,
∵ ,∴
,∴ ,
,
∴ ………………………………………………………………10分
………………………………………………………………10分
方法二:由(2)解法2知,平面 的一个法向量为
的一个法向量为 ……………………8分
……………………8分
又∵
∴点 到平面
到平面 的距离为
的距离为
 …………………………………10分
…………………………………10分
其余方法请酌情给分!!

 阅读快车系列答案
阅读快车系列答案 (2)若
(2)若 ,底面
,底面 是平行四边形,点
是平行四边形,点 在平面
在平面 在
在 边上,且
边上,且 ,
,
 .
.
 是
是 的中点,求异面直线
的中点,求异面直线 与
与 所成角的余弦值;
所成角的余弦值; 在棱
在棱 .求
.求 的值.
的值. ,底面
,底面 为菱形,
为菱形, 平面
平面 ,
, 是
是 的中点,
的中点, 为线段
为线段 上一点.
上一点. ;
; 为
为 上的动点,
上的动点, 与平面
与平面 所成最大角的
正切值为
所成最大角的
正切值为 ,若二面角
,若二面角 的余弦值为
的余弦值为 ,求
,求 的值。
的值。
 的底面是正方形,
的底面是正方形,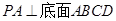 ,且
,且 ,点
,点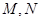 分别在侧棱
分别在侧棱 、
、 上,且
上,且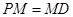 。
。
 ;
; ,求平面
,求平面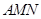 与平面
与平面 所成二面角的余弦值.
所成二面角的余弦值.  ,底面
,底面 为菱形,
为菱形, ⊥平面
⊥平面 ,
, 、
、 分别是
分别是 、
、 的中点。
的中点。 ⊥
⊥ ;
; (Ⅱ)若
(Ⅱ)若 为
为 与平面
与平面 所成最大角的正切值为
所成最大角的正切值为 ,求二面角
,求二面角 的余弦值。
的余弦值。