题目内容
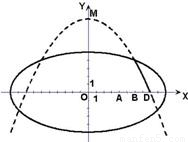
学校科技小组在计算机上模拟航天器变轨返回试验.设计方案如图:航天器运行(按顺时针方向)的轨迹方程为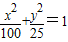 ,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以y轴为对称轴、
,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以y轴为对称轴、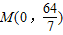 为顶点的抛物线的实线部分,降落点为D(8,0).观测点A(4,0)、B(6,0)同时跟踪航天器.
为顶点的抛物线的实线部分,降落点为D(8,0).观测点A(4,0)、B(6,0)同时跟踪航天器.(1)求航天器变轨后的运行轨迹所在的曲线方程;
(2)试问:当航天器在x轴上方时,观测点A、B测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
【答案】分析:(1)由题意变轨之后轨迹为开口向上的抛物线,所以利用待定系数法可以先设出方程,再利用条件建立未知数的方程进而求解;
(2)由题意及图形可知变轨点C实质为两圆锥曲线的交点,故联立两方程即可求解.
解答:解:(1)设曲线方程为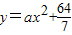 ,
,
由题意可知,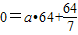 .
.
∴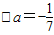 .
.
∴曲线方程为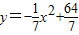 .
.
(2)设变轨点为C(x,y),根据题意可知
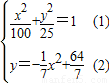
得4y2-7y-36=0,y=4或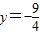 (不合题意,舍去).
(不合题意,舍去).
∴?y=4.
得x=6或x=-6(不合题意,舍去).
∴?C点的坐标为(6,4),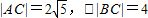 .
.
答:当观测点A、B测得AC、BC距离分别为 时,应向航天器发出变轨指令.
时,应向航天器发出变轨指令.
点评:(1)此问重点考查了抛物线的定义及其标准方程,还考查了求解方程当知道方程的类别利用待定系数法求解方程的思想;
(2)此问重点考查了两方程的交点求解的方法应该把两个方程进行联立求解的方法.
(2)由题意及图形可知变轨点C实质为两圆锥曲线的交点,故联立两方程即可求解.
解答:解:(1)设曲线方程为
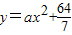 ,
,由题意可知,
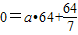 .
.∴
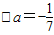 .
.∴曲线方程为
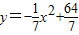 .
.(2)设变轨点为C(x,y),根据题意可知
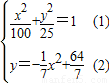
得4y2-7y-36=0,y=4或
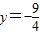 (不合题意,舍去).
(不合题意,舍去).∴?y=4.
得x=6或x=-6(不合题意,舍去).
∴?C点的坐标为(6,4),
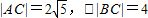 .
.答:当观测点A、B测得AC、BC距离分别为
 时,应向航天器发出变轨指令.
时,应向航天器发出变轨指令.点评:(1)此问重点考查了抛物线的定义及其标准方程,还考查了求解方程当知道方程的类别利用待定系数法求解方程的思想;
(2)此问重点考查了两方程的交点求解的方法应该把两个方程进行联立求解的方法.

练习册系列答案
相关题目
 学校科技小组在计算机上模拟航天器变轨返回试验.设计方案如图:航天器运行(按顺时针方向)的轨迹方程为
学校科技小组在计算机上模拟航天器变轨返回试验.设计方案如图:航天器运行(按顺时针方向)的轨迹方程为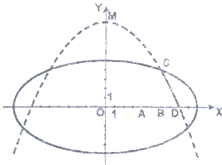 (2006•蚌埠二模)“神六”上天并顺利返回,让越来越多的青少年对航天技术发生了兴趣.某学校科技小组在计算机上模拟航天器变轨返回试验,设计方案
(2006•蚌埠二模)“神六”上天并顺利返回,让越来越多的青少年对航天技术发生了兴趣.某学校科技小组在计算机上模拟航天器变轨返回试验,设计方案
 学校科技小组在计算机上模拟航天器变轨返回试验. 设计方案如图:航天器运行(按顺时针方向)的轨迹方程为
学校科技小组在计算机上模拟航天器变轨返回试验. 设计方案如图:航天器运行(按顺时针方向)的轨迹方程为