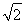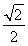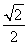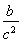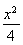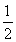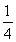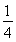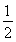题目内容
已知n∈N*，数列{dn}满足dn＝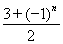
，数列{an}满足an＝d1＋d2＋d3＋…＋d2n.又知数列{bn}中，b1＝2，且对任意正整数m，n，
.
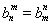(1)求数列{an}和数列{bn}的通项公式；
(2)将数列{bn}中的第a1项，第a2项，第a3项，…，第an项删去后，剩余的项按从小到大的顺序排成新数列{cn}，求数列{cn}的前2013项和T2013.
（1）an＝3n，bn＝2n.（2）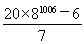
【解析】(1)∵dn＝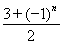
，∴an＝d1＋d2＋d3＋…＋d2n＝
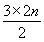＝3n.
又由题知，令m＝1时，则b2＝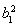
＝22，b3＝
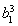＝23，…，bn＝
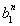＝2n，
若bn＝2n，则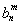
＝2nm，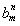
＝2mn，所以
＝
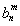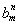恒成立；
若bn≠2n，当m＝1时，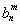
＝
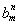不成立，所以bn＝2n.
(2)由题知将数列{bn}中的第3项、第6项、第9项…删去后构成的新数列{cn}中的奇数项与偶数项仍成等比数列，首项分别是b1＝2，b2＝4，公比均是8，
T2013＝(c1＋c3＋c5＋…＋c2013)＋(c2＋c4＋c6＋…＋c2012)
＝
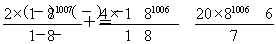
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
