题目内容
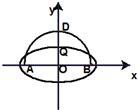 如图,ADB为半圆,AB为直径,O为圆心,
如图,ADB为半圆,AB为直径,O为圆心,| AB |
| OD |
(1)建立适当的坐标系,求曲线C的方程;
(2)过点D的直线l与曲线C相交于不同的两点M、N,求△OMN面积的最大值.
分析:(1)以AB和OD所在的直线为x轴、y轴,O为原点,由题中的条件得:PA|+|PB|=|QA|+|QB|=2
>|AB|=4,曲线C是以A、B为焦点的椭圆,待定系数法求椭圆的方程.
(2)设直线y=kx+2,代入曲线方程,由判别式大于0得k2的范围,利用根与系数的关系,求出点O到直线MN的距离,用弦长公式求得MN的长度,代入三角形面积公式,再利用基本不等式求出面积的最大值.
| 5 |
(2)设直线y=kx+2,代入曲线方程,由判别式大于0得k2的范围,利用根与系数的关系,求出点O到直线MN的距离,用弦长公式求得MN的长度,代入三角形面积公式,再利用基本不等式求出面积的最大值.
解答:解:(1)以AB和OD所在的直线为x轴、y轴,O为原点,
建立直角坐标系,∵|AB|=4,∴A(-2,0),B(2,0),D(0,2).
∴|PA|+|PB|=|QA|+|QB|=2
>|AB|=4,
∴曲线C是以A、B为焦点的椭圆,其长轴长2a=2
,2c=4,∴曲线C的方程为
+y2=1.
(2)设直线y=kx+2,代入曲线方程得(1+5k2)+20kx+15=0.
设M(x1,y1),N(x2,y2),则△=(20k)2-4(1+5k2)•15>0,∴k2>
.
∵
,
点O到直线MN的距离d=
,又|MN|=
|x1-x2|=
,
∴S△OMN=
|MN|•d=
•
•
=
.
设
=m,
∵k2>
,
∴k2=
,
∴S△OMN=
≤
=
(m>0),当且仅当m=
即m=2
时等号成立,
此时k2=
,
∴S△OMN的最大值为
.
建立直角坐标系,∵|AB|=4,∴A(-2,0),B(2,0),D(0,2).
∴|PA|+|PB|=|QA|+|QB|=2
| 5 |
∴曲线C是以A、B为焦点的椭圆,其长轴长2a=2
| 5 |
| x2 |
| 5 |
(2)设直线y=kx+2,代入曲线方程得(1+5k2)+20kx+15=0.
设M(x1,y1),N(x2,y2),则△=(20k)2-4(1+5k2)•15>0,∴k2>
| 3 |
| 5 |
∵
|
点O到直线MN的距离d=
| 1 | ||
|
| 1+k2 |
| 1+k2 |
| ||
| 1+5k2 |
∴S△OMN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1+k2 |
| ||
| 1+5k2 |
| 2 | ||
|
2
| ||
| 1+5k2 |
设
| 25k2-15 |
∵k2>
| 3 |
| 5 |
∴k2=
| m2+15 |
| 25 |
∴S△OMN=
| 10m |
| m2+20 |
| 10 | ||||
2
|
| ||
| 2 |
| 20 |
| m |
| 5 |
此时k2=
| 7 |
| 5 |
∴S△OMN的最大值为
| ||
| 2 |
点评:本题考查用待定系数法求椭圆的标准方程,点到直线的距离公式及基本不等式的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,
如图,
 如图,
如图,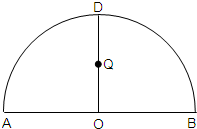 如图,ADB为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变
如图,ADB为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变