题目内容
在锐角三角形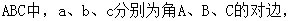 且
且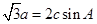
(1)确定角C的大小:
(2)若c=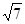 ,且△ABC的面积为
,且△ABC的面积为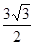
 ,求a+b的值
,求a+b的值
【答案】
(1) ;(2)
;(2)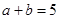 。
。
【解析】
试题分析:(1)利用正弦定理,化边为角,得到角C的值。
(2) 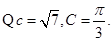 由面积公式得,得到ab的值,进而结合余弦定理得到a,b,的值。
由面积公式得,得到ab的值,进而结合余弦定理得到a,b,的值。
(1)由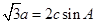 及正弦定理得,
及正弦定理得,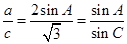
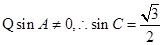
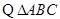 是锐角三角形,
是锐角三角形,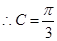
(2)解法1: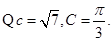 由面积公式得
由面积公式得
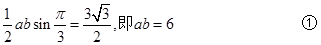
由余弦定理得
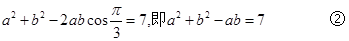
由②变形得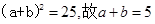
解法2:前同解法1,联立①、②得
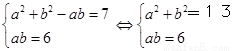
消去b并整理得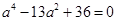 解得
解得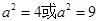
所以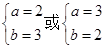 故
故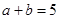
考点:本试题主要考查了解三角形的运用。
点评:解决该试题的关键是灵活运用正弦定理得到角C的值,并能利用余弦定理来得到ab,的值。注意前后的联系,对于两个定理的熟练运用。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目