题目内容
若定义在R上的偶函数
上单调递减，且
，则不等式
的解集是（ ）
A． | B． |
C． | D． |
D
解析试题分析：因为
是偶函数，所以
，又因为上单调递减，所以在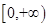
上单调递增。所以当
时， >0；当
时，<0..
由得
，所以
，所以等式的解集是。
考点：函数的奇偶性；函数的单调性。
点评：（1）本题给出函数为偶函数且在负数范围内是减函数，求不等式f（x）＞0的解集．考查了函数单调性和奇偶性的综合的知识，属于基础题．（2）奇函数在关于原点对称的两个区间上的单调性相同，偶函数在关于原点对称的两个区间上的单调性相反。
练习册系列答案
相关题目
方程
在区间
上有解，则实数
的取值范围是 （ ）
A． | B．  | C． | D． |
f(x)＝－x2＋mx在(－∞，1]上是增函数，则m的取值范围是( )
| A．{2} | B．(－∞，2] | C．[2，＋∞) | D．(－∞，1] |
设f(x)=
,用二分法求方程=0在
内近似值的过程中得f(1) < 0,f(1.5) > 0,f (1.25) < 0,则方程的根落在区间（ ）
| A．（1，1.25） | B．（1.25，1.5） | C．（1.5，2） | D．不能确定 |
已知函数
,且
.则（ ）
A． | B． |
C． | D． |
函数
的值域是（ ）
A． | B． | C． | D． |
函数
是（ ）
A．奇函数，且在 上是增函数 | B．奇函数，且在上是减函数 |
| C．偶函数，且在上是增函数 | D．偶函数，且在上是减函数 |
下列函数中既不是奇函数也不是偶函数的是（ ）
A． | B． |
C． | D． |
已知函数
，若
互不相等，且
，
则
的取值范围是( )
| A．（1，10） | B．（5，6） | C．（10，12） | D．（20，24） |