题目内容
已知△AOB的一个顶点为抛物线y2=2x的顶点O,A、B两点都在抛物线上,且∠AOB=90°
(1)证明直线AB必过一定点;
(2)求△AOB面积的最小值.
答案:
解析:
解析:
解析:设直线OA的方程为y=kx,则直线OB的方程为y=![]() ,由
,由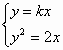 解得A(
解得A(![]() ,
,![]() )(k≠0).
)(k≠0).
同理由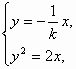 可得B(2k2,-2k),∴直线AB的方程为y+2k=
可得B(2k2,-2k),∴直线AB的方程为y+2k=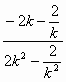 (x-2k2),化简得x-(
(x-2k2),化简得x-(![]() )y-2=0.
)y-2=0.
显然过定点P(2,0).
(2)设直线AB方程为x=my+2,代入y2=2x,得y2-2my-4=0,∴y1+y2=2m,y1·y2=-4
∴|y1-y2|=![]() ,
,
∴S△AOB=![]() ·|OP|·|y1-y2|=
·|OP|·|y1-y2|=![]() ×2×.
×2×.
显然,当m=0时,S△AOB的最小值为4.

练习册系列答案
相关题目