题目内容
在等比数列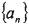 中,
中,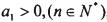 ,且
,且 ,又
,又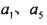 的等比中项为16.
的等比中项为16.
(I)
求数列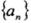 的通项公式:
的通项公式:
(II) 设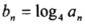 ,数列
,数列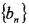 的前项和为
的前项和为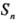 ,是否存在正整数k,使得
,是否存在正整数k,使得 对任意
对任意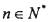 恒成立.若存在,求出正整数k的最小值;不存在,请说明理由.
恒成立.若存在,求出正整数k的最小值;不存在,请说明理由.
【答案】
(Ⅰ) 由题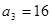 ,又
,又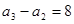 ,则
,则
∴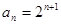 ……………………….…
……………………….… ..4分
..4分
(Ⅱ) 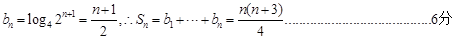
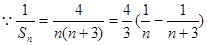
 …….10分
…….10分
所以正整数 可取最小值3
可取最小值3
【解析】略

练习册系列答案
相关题目
 中,
中, ,且
,且 是
是 和
和 的等差中项.
的等差中项. 满足
满足 ,求
,求 项和
项和 .
. 中,若公比
中,若公比 ,且前3项之和等于21,则该数列的通项公式
,且前3项之和等于21,则该数列的通项公式
 中,
中, ,且
,且 ,则
,则 的最小值为
的最小值为  中,若公比
中,若公比 ,且
,且 ,则该数列的通项公式
,则该数列的通项公式 .
.  中,
中, ,且
,且 ,则
,则 的最小值为 ★ .
的最小值为 ★ .