题目内容
如果函数f(x)=ax(ax-3a2-1)(a>0且a≠1)在区间[0,+∞)上是增函数,那么实数a的取值范围是 ________.
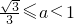
分析:先利用换元法将函数化成一元二次函数,然后将a与1进行比较,分别研究,利用符合函数的单调性的知识进行建立关系式求解即可.
解答:令ax=t则f(x)=ax(ax-3a2-1)可转化成
y=t2-(3a2+1)t,其对称轴为
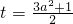 >0
>0当a>1时,t>1,要使函数y=t2-(3a2+1)t在(1,+∞)上是增函数
则
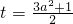 <1,故不存在a使之成立;
<1,故不存在a使之成立;当0<a<1时,0<t<1,要使函数y=t2-(3a2+1)t在(0,1)上是减函数
则
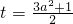 >1,故
>1,故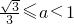
综上所述,
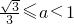
故答案为:
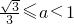 .
.点评:本题主要考查了复合函数单调性的应用,以及换元法的运用,在高考中关于复合函数的单调性有所弱化,属于基础题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
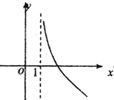
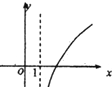
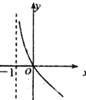

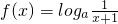 的图象大致是
的图象大致是



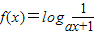 的图象大致是( )
的图象大致是( )



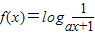 的图象大致是( )
的图象大致是( )



 的图象大致是( )
的图象大致是( )