题目内容
在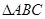 中,内角
中,内角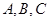 的对边分别为
的对边分别为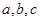 ,并且
,并且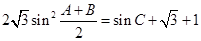 .
.
(1)求角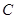 的大小;
的大小;
(2)若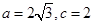 ,求
,求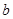 .
.
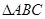 中,内角
中,内角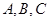 的对边分别为
的对边分别为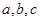 ,并且
,并且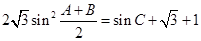 .
.(1)求角
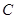 的大小;
的大小;(2)若
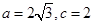 ,求
,求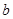 .
.(1) 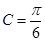 ,(2)
,(2) 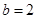 或
或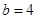 .
.
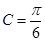 ,(2)
,(2) 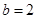 或
或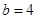 .
.本题考查解三角形中的余弦定理的运用,利用倍角公式、两角和与差的余弦公式进行三角恒等变形.考查运算能力,考查公式的灵活运用能力.第一问,先利用 将角
将角 转化为
转化为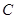 角,再利用降幂公式变形,化简后再利用两角和的余弦公式变形,在三角形内判断角
角,再利用降幂公式变形,化简后再利用两角和的余弦公式变形,在三角形内判断角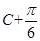 的范围,通过
的范围,通过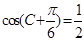 求角;第二问,利用第一问的结论,利用余弦定理
求角;第二问,利用第一问的结论,利用余弦定理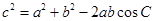 列出表达式,解方程求出
列出表达式,解方程求出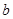 边.
边.
试题分析:(1) ∵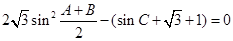 ,
,
∴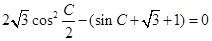 ,(2分)
,(2分)
即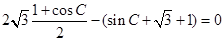 ,(3分)
,(3分)
即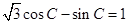 ,亦即
,亦即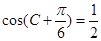 .(5分)
.(5分)
∵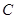 为
为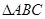 的内角,
的内角,
∴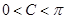 ,∴
,∴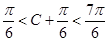 .(7分)
.(7分)
从而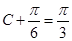 ,∴
,∴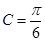 .(8分)
.(8分)
(2)∵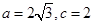 ,
,
∴由余弦定理得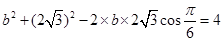 .(10分)
.(10分)
即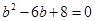 ,
,
解得: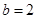 或
或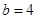 .(12分)
.(12分)
 将角
将角 转化为
转化为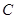 角,再利用降幂公式变形,化简后再利用两角和的余弦公式变形,在三角形内判断角
角,再利用降幂公式变形,化简后再利用两角和的余弦公式变形,在三角形内判断角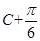 的范围,通过
的范围,通过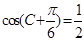 求角;第二问,利用第一问的结论,利用余弦定理
求角;第二问,利用第一问的结论,利用余弦定理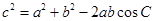 列出表达式,解方程求出
列出表达式,解方程求出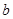 边.
边.试题分析:(1) ∵
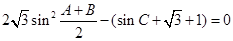 ,
,∴
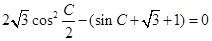 ,(2分)
,(2分)即
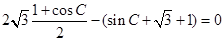 ,(3分)
,(3分)即
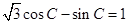 ,亦即
,亦即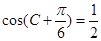 .(5分)
.(5分)∵
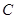 为
为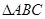 的内角,
的内角,∴
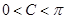 ,∴
,∴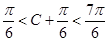 .(7分)
.(7分)从而
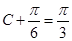 ,∴
,∴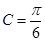 .(8分)
.(8分)(2)∵
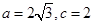 ,
,∴由余弦定理得
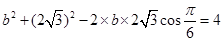 .(10分)
.(10分)即
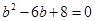 ,
,解得:
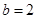 或
或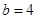 .(12分)
.(12分)
练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
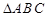 中,角
中,角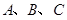 所对的边分别为
所对的边分别为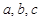 ,且
,且 ,
, ,求
,求 的取值范围.
的取值范围.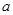 、
、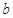 是方程
是方程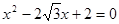 的两根,角
的两根,角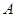 、
、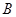 满足
满足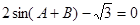 ,求角
,求角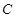 的度数,边
的度数,边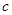 的长度及
的长度及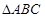 的面积.
的面积.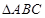 中,角
中,角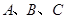 对边分别是
对边分别是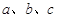 ,且满足
,且满足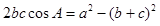 .
.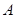 的大小;
的大小;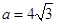 ,
,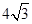 ;求
;求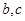 .
.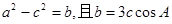 ,则b= .
,则b= .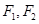 是双曲线
是双曲线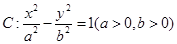 的左、右焦点,过
的左、右焦点,过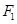 的直线与双曲线的左、右两支分别交于
的直线与双曲线的左、右两支分别交于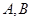 两点.若
两点.若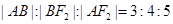 ,则双曲线的离心率为____ .
,则双曲线的离心率为____ .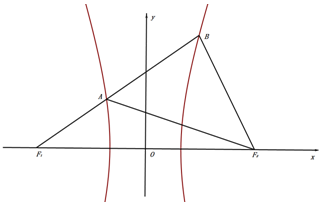
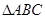 中,
中,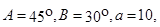 则
则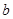 等于
等于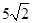
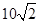
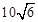
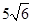
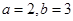 ,则边长
,则边长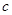 的取值范围是_________
的取值范围是_________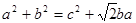 ,则
,则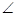 C=( )
C=( )