题目内容
有下列各式:1+| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 7 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 15 |
分析:观察各式左边为
的和的形式,项数分别为:3,7,15,故可猜想第n个式子中应有2n+1-1项,
不等式右侧分别写成
,
,
故猜想第n个式子中应为
,由此可写出一般的式子.
| 1 |
| n |
不等式右侧分别写成
| 2 |
| 2 |
| 3 |
| 2 |
| 4 |
| 2 |
| n+1 |
| 2 |
解答:解:观察各式左边为
的和的形式,项数分别为:3,7,15,故可猜想第n个式子中应有2n+1-1项,
不等式右侧分别写成
,
,
故猜想第n个式子中应为
,
按此规律可猜想此类不等式的一般形式为:1+
+
++
>
(n∈N*)
故答案为:1+
+
++
>
(n∈N*)
| 1 |
| n |
不等式右侧分别写成
| 2 |
| 2 |
| 3 |
| 2 |
| 4 |
| 2 |
| n+1 |
| 2 |
按此规律可猜想此类不等式的一般形式为:1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n+1-1 |
| n+1 |
| 2 |
故答案为:1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n+1-1 |
| n+1 |
| 2 |
点评:本题考查归纳推理、考查观察、分析、解决问题的能力.

练习册系列答案
相关题目
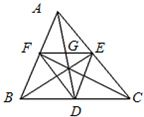 如图,在△ABC中,D、E、F分别是各边的中点,AD交EF于点G,则下列各式能表示向量
如图,在△ABC中,D、E、F分别是各边的中点,AD交EF于点G,则下列各式能表示向量