题目内容
有四个数,其中前三个数成等差数列,后三个数成等比数列,并且第一个数与第四个数的和是16,第二个数与第三个数的和是12.求这四个数.
解法一:设四个数依次为a-d,a,a+d,![]() ,
,
依题意,有
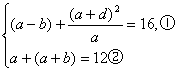
由②式得d=12-2a. ③
将③代入①得a-12+2a+![]() =16.
=16.
整理得a2-13a+36=0.
∴a1=4,a2=9.
代入③得d1=4,d2=-6.
从而所求四个数为0,4,8,16或15,9,3,1.
解法二:设四个数依次为x,y,12-y,16-x.
依题意,有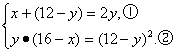
由①得x=3y-12. (3)
将③代入②并整理得y2-13y+36=0.
解得y1=4,y2=9.
∴x1=0,x2=15.
从而所求四个数为0,4,8,16或15,9,3,1.
解法三:设这四个数为2a-aq,a,aq,aq2,
则由条件知
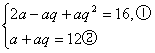
由②得a=![]() ,代入①得3q2-7q+2=0,
,代入①得3q2-7q+2=0,
解得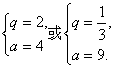
从而所求四个数为0,4,8,16或15,9,3,1.
温馨提示
三数成等差数列常把三数设为a-d,a,a+d,如解法一;
解法二为了减少未知量数目,仅设前两数为x,y,后两数用x,y表示;
在已知三数之积的条件下,将等比数列三项设为![]() ,a,aq是恰当的设法.
,a,aq是恰当的设法.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目