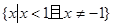题目内容
不等式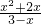 ≥0的解集为
≥0的解集为
- A.(-∞,-2]∪[0,3)
- B.(-2,0)∪(3,+∞)
- C.[-2,0]∪[3,+∞)
- D.(-∞,0]∪(3,+∞)
A
分析:把原不等式的分子分解因式,在不等式两边都除以-1后,可利用两数相除异号得负转化为两个不等式组,分别求出不等式组的解集,即可求出原不等式的解集.
解答:由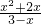 ≥0,分解因式得:
≥0,分解因式得: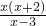 ≤0,
≤0,
可化为: 或
或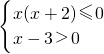 ,
,
分别解得:x≤-2或0≤x<3;无解,
所以原不等式的解集为(-∞,-2]∪[0,3).
故选A.
点评:此题考查了一元二次不等式及其他不等式的解法,考查了转化的思想,是一道综合题.
分析:把原不等式的分子分解因式,在不等式两边都除以-1后,可利用两数相除异号得负转化为两个不等式组,分别求出不等式组的解集,即可求出原不等式的解集.
解答:由
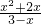 ≥0,分解因式得:
≥0,分解因式得: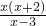 ≤0,
≤0,可化为:
 或
或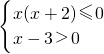 ,
,分别解得:x≤-2或0≤x<3;无解,
所以原不等式的解集为(-∞,-2]∪[0,3).
故选A.
点评:此题考查了一元二次不等式及其他不等式的解法,考查了转化的思想,是一道综合题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
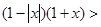 0的解集为
0的解集为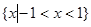 (B)
(B)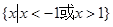 (C)
(C) (D)
(D)