题目内容
比较下列各组中两个代数式的大小:
⑴x2+3与3x ;
⑵已知a,b为正数,且a≠b,比较a3 +b3与a2b+ab2
⑴x2+3与3x ;
⑵已知a,b为正数,且a≠b,比较a3 +b3与a2b+ab2
解:(1)x2+3-3x
= x2-3x+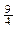 -
-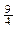 +3
+3
=(x-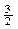 )2 +
)2 +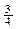 >0
>0
∴ x2+3>3x
(2)a3 +b3-(a2b+ab2)
=(a3-a2b)+(b3-ab2)
= a2(a-b)+ b2(b-a)
=( a2-b2)( a-b)
=( a-b)2( a+b)
∵ a,b为正数,且a≠b
∴( a-b)2>0, a+b>0
∴( a-b)2( a+b)>0
∴ a3 +b3>a2b+ab2
= x2-3x+
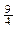 -
-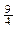 +3
+3 =(x-
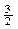 )2 +
)2 +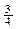 >0
>0∴ x2+3>3x
(2)a3 +b3-(a2b+ab2)
=(a3-a2b)+(b3-ab2)
= a2(a-b)+ b2(b-a)
=( a2-b2)( a-b)
=( a-b)2( a+b)
∵ a,b为正数,且a≠b
∴( a-b)2>0, a+b>0
∴( a-b)2( a+b)>0
∴ a3 +b3>a2b+ab2
略

练习册系列答案
相关题目
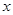 ,
,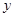 满足约束条件
满足约束条件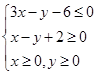 ,若目标函数
,若目标函数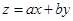 (
(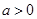 ,
,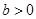 )的最大值为12,则
)的最大值为12,则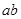 的取值范围是( )
的取值范围是( )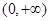
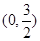
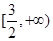

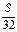
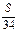
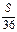
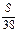
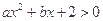 的解集是
的解集是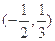 ,求
,求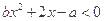 的解集;
的解集;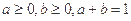 ,求
,求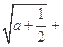
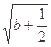 的取值范围.
的取值范围.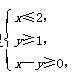 则2x+y取最小值时的最优解是
则2x+y取最小值时的最优解是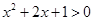
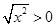
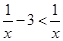
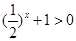
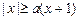 对任意的实数x都成立,则实数
对任意的实数x都成立,则实数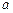 的取值范围是______
的取值范围是______ ,都有
,都有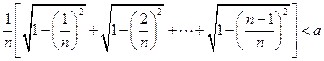
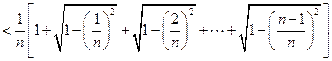 ,则实数
,则实数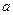 =_________.
=_________. 出以下四个命题:
出以下四个命题: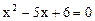 ,则x=2或x=3;
,则x=2或x=3; +y是奇数,则x,y中一个是奇数,一个是偶数.那么( )
+y是奇数,则x,y中一个是奇数,一个是偶数.那么( )