题目内容
（本小题满分12分）求抛物线
与直线
围成的平面图形的面积.
与直线围成的平面图形的面积.解: 由方程组
解出抛物线和直线的交点为（2, 2）及（8, －4）…2分
解法1:选x作为积分变量，由图可看出S=A1+A2
在A1部分：由于抛物线的上半支方程为
，下半支方程为
所以……3分
……………………………………5分
…………………………………………………………7分
…………………………………………………9分
……………………………………………11分
于是：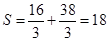
………………………………………………………………12分
解法二: 选y作积分变量，将曲线方程写为
及
………………………………………………………………2分
…………………………………………………………6分
……………………………………………………………10分
……………………………………………………………12分
解出抛物线和直线的交点为（2, 2）及（8, －4）…2分解法1:选x作为积分变量，由图可看出S=A1+A2
在A1部分：由于抛物线的上半支方程为
，下半支方程为所以……3分 ……………………………………5分 …………………………………………………………7分 …………………………………………………9分……………………………………………11分于是：
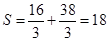………………………………………………………………12分解法二: 选y作积分变量，将曲线方程写为
及 ………………………………………………………………2分 …………………………………………………………6分 ……………………………………………………………10分 ……………………………………………………………12分略
练习册系列答案
阅读快车系列答案
相关题目
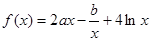在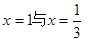
处都取得极值．
、
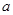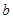的值；
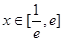时，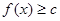
恒成立，求实数
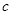的取值范围．
= 
的值为（ ）
＝________.
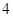
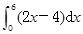，借助定积分表达围成的封闭图形的面积（ ）
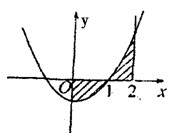
与直线
所围成的封闭图形的面积是
=_________
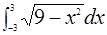，则k=( )