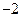题目内容
(本小题满分14分)
已知二次函数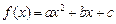 , 满足
, 满足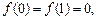 且
且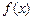 的最小值是
的最小值是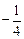 .
.
(Ⅰ)求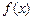 的解析式;
的解析式;
(Ⅱ)设直线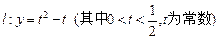 ,若直线
,若直线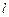 与
与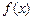 的图象以及
的图象以及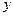 轴这二条直线和一条曲线所围成封闭图形的面积是
轴这二条直线和一条曲线所围成封闭图形的面积是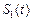 , 直线
, 直线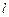 与
与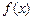 的图象以及直线
的图象以及直线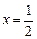 这二条直线和一条曲线所围成封闭图形的面积是
这二条直线和一条曲线所围成封闭图形的面积是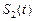 ,已知
,已知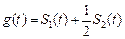 ,当
,当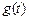 取最小值时,求
取最小值时,求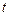 的值.
的值.
已知二次函数
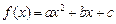 , 满足
, 满足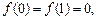 且
且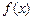 的最小值是
的最小值是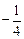 .
.(Ⅰ)求
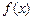 的解析式;
的解析式;(Ⅱ)设直线
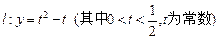 ,若直线
,若直线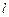 与
与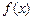 的图象以及
的图象以及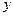 轴这二条直线和一条曲线所围成封闭图形的面积是
轴这二条直线和一条曲线所围成封闭图形的面积是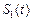 , 直线
, 直线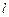 与
与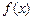 的图象以及直线
的图象以及直线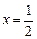 这二条直线和一条曲线所围成封闭图形的面积是
这二条直线和一条曲线所围成封闭图形的面积是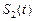 ,已知
,已知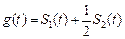 ,当
,当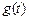 取最小值时,求
取最小值时,求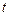 的值.
的值.(Ⅰ)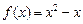
(Ⅱ)当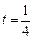 时,
时,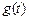 有最小值.
有最小值.
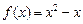
(Ⅱ)当
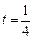 时,
时,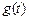 有最小值.
有最小值.解: (1)由二次函数图象的对称性, 可设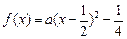 ,又
,又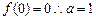
故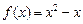 …………………5分
…………………5分
(2) 据题意, 直线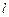 与
与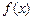 的图象的交点坐标为
的图象的交点坐标为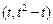 ,由定积分的几何意义知
,由定积分的几何意义知
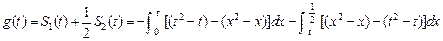
=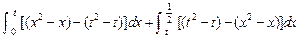
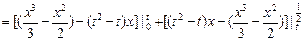
=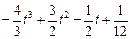
而
令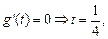 或
或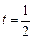 (不合题意,舍去)
(不合题意,舍去)
当
故当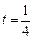 时,
时,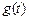 有最小值.……………………………………………………14分
有最小值.……………………………………………………14分
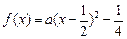 ,又
,又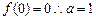
故
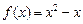 …………………5分
…………………5分(2) 据题意, 直线
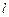 与
与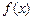 的图象的交点坐标为
的图象的交点坐标为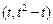 ,由定积分的几何意义知
,由定积分的几何意义知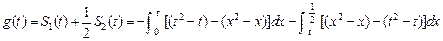
=
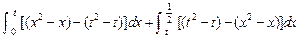
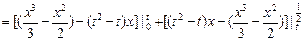
=
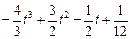
而

令
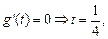 或
或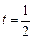 (不合题意,舍去)
(不合题意,舍去)当

故当
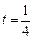 时,
时,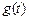 有最小值.……………………………………………………14分
有最小值.……………………………………………………14分
练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
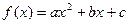 ,
,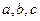 为实数,且当
为实数,且当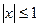 时,恒有
时,恒有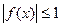 ;(I)证明:
;(I)证明: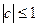 ;
;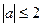 ;
;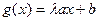
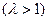 ,求证:当
,求证:当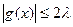 .
.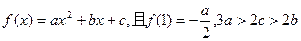 ,
,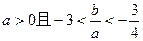 ;
;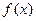 在区间(0,2)内至少有一个零点;
在区间(0,2)内至少有一个零点;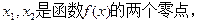 求
求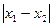 的取值范围.
的取值范围.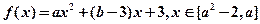 是偶函数,则
是偶函数,则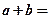 _____________.
_____________.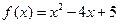 在区间 [0,
在区间 [0,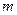 ]上的最大值为5,最小值为1,则
]上的最大值为5,最小值为1,则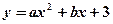 在
在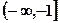 上是增函数,在
上是增函数,在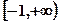 上是
上是 减函数,则(
减函数,则(  )
)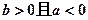
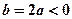
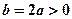

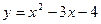 的定义域为[0,m],值域为
的定义域为[0,m],值域为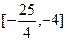 ,则m的取值范围是( )
,则m的取值范围是( )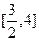
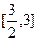
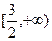
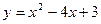 在区间
在区间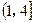 上的值域是
上的值域是 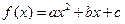 ,
,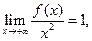
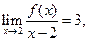 则
则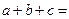 ( )
( )