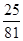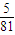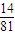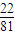题目内容
一袋中有红、黄、蓝三种颜色的小球各一个,每次从中取出一个,记下颜色后放回,当三种颜色的球全部取出时停止取球,则恰好取5次球时停止取球的概率为
.
| 14 |
| 81 |
| 14 |
| 81 |
分析:首先由分步计数原理可得,从3个小球中有放回的连续5次任取1球的情况数目;分析可得若恰好取5次球时停止取球,则在前4次取球中,前两种颜色都至少取得1次,在第5次恰好取出第三种颜色,可以先选出2种颜色在前4次中取到,再用排除法分析得到前4次取球中,这两种颜色都至少取得1次的情况数目,而第5次恰好取出第三种颜色有1种情况,由分步计数原理可得恰好取5次球时停止取球的情况数目,由等可能事件的概率公式,计算可得答案.
解答:解:根据题意,从3个小球中有放回的连续5次任取1球,有35=243种情况,
若恰好取5次球时停止取球,则在前4次中,前两种颜色都至少取得1次,在第5次恰好取出最后一种即第三种颜色,
在前4次中,只取2种颜色,有C32=3种情况,
且这两种颜色都至少取得1次,
前4次取球中,只取这2种颜色有24种情况,其中颜色相同的有2种,
则前4次取球有3×(24-2)=42种情况,
第5次恰好取出第三种颜色有1种情况,
故恰好取5次球时停止取球有42种情况,
则其概率P=
=
.
若恰好取5次球时停止取球,则在前4次中,前两种颜色都至少取得1次,在第5次恰好取出最后一种即第三种颜色,
在前4次中,只取2种颜色,有C32=3种情况,
且这两种颜色都至少取得1次,
前4次取球中,只取这2种颜色有24种情况,其中颜色相同的有2种,
则前4次取球有3×(24-2)=42种情况,
第5次恰好取出第三种颜色有1种情况,
故恰好取5次球时停止取球有42种情况,
则其概率P=
| 42 |
| 243 |
| 14 |
| 81 |
点评:本题考查等可能事件的概率,涉及排列、组合与分步计数原理的应用,注意本题是有放回抽取.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
一袋中有红、黄、蓝三种颜色的小球各一个,每次从中取出一个,记下颜色后放回,当三种颜色的球全部取出时停止取球,则恰好取5次球时停止取球的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 B.
B. C.
C.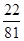 D.
D.