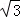题目内容
如图放置的边长为
的正△
沿边长为
的正方形
的各边内侧逆时针方向滚动．当△沿正方形各边滚动一周后，回到初始位置时，点
的轨迹长度是( )
A． | B． | C． | D． |
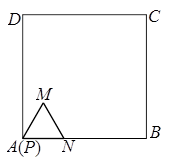
B
解析试题分析：由题意得：当△沿正方形一边滚动时，点的轨迹为两个圆弧，其对应圆半径皆为1，圆心角为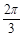
，因此点的轨迹长度是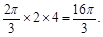
考点：动点轨迹
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
若直线
与圆
相切，且
为锐角，则这条直线的斜率是( )
A． | B． | C． | D． |
已知
，则直线
与圆：
的位置关系是( )．
| A．相交 | B．相切 | C．相离 | D．不能确定 |
已知圆C：x2＋(y－3)2＝4，过A(－1,0)的直线l与圆C相交于P，Q两点，若|PQ|＝2
，则直线l的方程为( )
| A．x＝－1或4x＋3y－4＝0 |
| B．x＝－1或4x－3y＋4＝0 |
| C．x＝1或4x－3y＋4＝0 |
| D．x＝1或4x＋3y－4＝0 |
[2012·辽宁高考]将圆x2＋y2－2x－4y＋1＝0平分的直线是( )
| A．x＋y－1＝0 | B．x＋y＋3＝0 |
| C．x－y＋1＝0 | D．x－y＋3＝0 |
已知点M(a,b)在圆
外, 则直线ax + by = 1与圆O的位置关系是
| A．相切 | B．相交 | C．相离 | D．不确定 |
点P(4，－2)与圆x2＋y2＝4上任一点连线的中点轨迹方程是( )
| A．(x－2)2＋(y－1)2＝1 |
| B．(x＋2)2＋(y－1)2＝1 |
| C．(x－2)2＋(y＋1)2＝1 |
| D．(x－1)2＋(y＋2)2＝1 |
直线ax+by+c=0与圆x2+y2=4相交于A,B两点,若c2=a2+b2,O为坐标原点,则
·
=( )
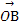| A．2 | B． | C．-2 | D．- |