题目内容
若非零不共线向量 、
、 满足|
满足| -
- |=|
|=| |,则下列结论正确的个数是________.
|,则下列结论正确的个数是________.
①向量 、
、 的夹角恒为锐角; ②2|
的夹角恒为锐角; ②2| |2>
|2> •
• ; ③|2
; ③|2 |>|
|>| -2
-2 |; ④|2
|; ④|2 |<|2
|<|2 -
- |.
|.
3
分析:对于①,利用已知条件,推出向量 、
、 、
、 组成的三角形是等腰三角形,判定正误即可.
组成的三角形是等腰三角形,判定正误即可.
对于②,利用数量积公式,结合已知条件,判断正误. 对于③,通过平方以及向量的数量积判断正误.
对于④,|2 |<|2
|<|2 -
- |等价于 4|
|等价于 4| |cos<
|cos< ,
, ><|
><| |,不一定成立,说明正误即可.
|,不一定成立,说明正误即可.
解答:∵非零不共线向量 、
、 满足|
满足| -
- |=|
|=| |,∴向量
|,∴向量 、
、 、
、 组成的三角形是等腰三角形,
组成的三角形是等腰三角形,
且向量 为底边,故向量
为底边,故向量 、
、 的夹角恒为锐角,①正确.
的夹角恒为锐角,①正确.
②2| |2>
|2> •
• 等价于2|
等价于2| |2>|
|2>| |•|
|•| |•cos<
|•cos< ,
, >,等价于2|
>,等价于2| |>|
|>| |•cos<
|•cos< ,
, >.
>.
而由| -
- |=|
|=| |可得|
|可得| -
- |+|
|+| |=2|
|=2| |>|
|>| |>|
|>| |•cos<
|•cos< ,
, >,即 2|
>,即 2| |>|
|>| |•cos<
|•cos< ,
, >成立,
>成立,
故②正确.
③|2 |>|
|>| -2
-2 |等价于 4
|等价于 4 >
> -4
-4 +4
+4 ,等价于 4
,等价于 4 >
> ,
,
等价于 4| |•|
|•| |cos<
|cos< ,
, >>
>> ,等价于 4|
,等价于 4| |cos<
|cos< ,
, >>|
>>| |.
|.
而 2| |cos<
|cos< ,
, >=|
>=| |,∴4|
|,∴4| |cos<
|cos< ,
, >>|
>>| |成立,故正确.
|成立,故正确.
④|2 |<|2
|<|2 -
- |等价于 4
|等价于 4 <4
<4 -4
-4 +
+ ,等价于 4
,等价于 4 <
< ,
,
等价于 4| |cos<
|cos< ,
, ><|
><| |,不一定成立,所以④不正确.
|,不一定成立,所以④不正确.
故答案为 3.
点评:本题考查向量的数量积的应用,向量的模的求法,考查计算能力,属于中档题.
分析:对于①,利用已知条件,推出向量
 、
、 、
、 组成的三角形是等腰三角形,判定正误即可.
组成的三角形是等腰三角形,判定正误即可.对于②,利用数量积公式,结合已知条件,判断正误. 对于③,通过平方以及向量的数量积判断正误.
对于④,|2
 |<|2
|<|2 -
- |等价于 4|
|等价于 4| |cos<
|cos< ,
, ><|
><| |,不一定成立,说明正误即可.
|,不一定成立,说明正误即可.解答:∵非零不共线向量
 、
、 满足|
满足| -
- |=|
|=| |,∴向量
|,∴向量 、
、 、
、 组成的三角形是等腰三角形,
组成的三角形是等腰三角形,且向量
 为底边,故向量
为底边,故向量 、
、 的夹角恒为锐角,①正确.
的夹角恒为锐角,①正确.②2|
 |2>
|2> •
• 等价于2|
等价于2| |2>|
|2>| |•|
|•| |•cos<
|•cos< ,
, >,等价于2|
>,等价于2| |>|
|>| |•cos<
|•cos< ,
, >.
>.而由|
 -
- |=|
|=| |可得|
|可得| -
- |+|
|+| |=2|
|=2| |>|
|>| |>|
|>| |•cos<
|•cos< ,
, >,即 2|
>,即 2| |>|
|>| |•cos<
|•cos< ,
, >成立,
>成立,故②正确.
③|2
 |>|
|>| -2
-2 |等价于 4
|等价于 4 >
> -4
-4 +4
+4 ,等价于 4
,等价于 4 >
> ,
,等价于 4|
 |•|
|•| |cos<
|cos< ,
, >>
>> ,等价于 4|
,等价于 4| |cos<
|cos< ,
, >>|
>>| |.
|.而 2|
 |cos<
|cos< ,
, >=|
>=| |,∴4|
|,∴4| |cos<
|cos< ,
, >>|
>>| |成立,故正确.
|成立,故正确.④|2
 |<|2
|<|2 -
- |等价于 4
|等价于 4 <4
<4 -4
-4 +
+ ,等价于 4
,等价于 4 <
< ,
,等价于 4|
 |cos<
|cos< ,
, ><|
><| |,不一定成立,所以④不正确.
|,不一定成立,所以④不正确.故答案为 3.
点评:本题考查向量的数量积的应用,向量的模的求法,考查计算能力,属于中档题.

练习册系列答案
相关题目
 、
、 满足|
满足| -
- |=|
|=| |,则下列结论正确的个数是 .
|,则下列结论正确的个数是 . 、
、 的夹角恒为锐角; ②2|
的夹角恒为锐角; ②2| |2>
|2> •
• ; ③|2
; ③|2 |>|
|>| -2
-2 |; ④|2
|; ④|2 |<|2
|<|2 -
- |.
|. 、
、 满足|
满足| -
- |=|
|=|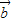 |,则下列结论正确的个数是( )
|,则下列结论正确的个数是( ) 、
、 的夹角恒为锐角;
的夹角恒为锐角; |2>
|2> •
• ;
; |>|
|>| -2
-2 |;
|; |<|2
|<|2 -
- |.
|. 、
、 满足|
满足| -
- |=|
|=| |,则下列结论正确的个数是( )
|,则下列结论正确的个数是( ) 、
、 的夹角恒为锐角;
的夹角恒为锐角; |2>
|2> •
• ;
; |>|
|>| -2
-2 |;
|; |<|2
|<|2 -
- |.
|. 、
、 满足|
满足| ﹣
﹣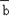 |=|
|=| |,则下列结论正确的个数是( )
|,则下列结论正确的个数是( ) 、
、 的夹角恒为锐角; ②2|
的夹角恒为锐角; ②2| |2>
|2>
 ; ③|2
; ③|2 |>|
|>| ﹣2
﹣2 |; ④|2
|; ④|2 |<|2
|<|2 ﹣
﹣ |.
|.