题目内容
 如图,弹簧挂着小球作上下振动,时间t(s)与小球相对平衡位置(即静止的位置)的高度h(cm)之间的函数关系式是h=2sin(4πt+
如图,弹簧挂着小球作上下振动,时间t(s)与小球相对平衡位置(即静止的位置)的高度h(cm)之间的函数关系式是h=2sin(4πt+| π |
| 4 |
| A、2,2 | ||
| B、4,2 | ||
C、4,
| ||
D、2,
|
分析:根据题中的解析式可得小球震动的幅度与周期,进而得到答案.
解答:解:因为时间t(s)与小球相对平衡位置的高度h(cm)之间的函数关系式是h=2sin(4πt+
)(t∈[0,+∞)),
所以小球的振幅是2,并且周期是
=
,
所以小球最高点与最低点的距离是4,每秒能往复振动的次数即频率为2.
故选B.
| π |
| 4 |
所以小球的振幅是2,并且周期是
| 2π |
| 4π |
| 1 |
| 2 |
所以小球最高点与最低点的距离是4,每秒能往复振动的次数即频率为2.
故选B.
点评:本题主要考查了三角函数的振幅、周期性及其求法.考查了学生分析问题和解决实际问题的能力.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
 如图,弹簧挂着小球作上下振动,时间t(s)与小球相对平衡位置(即静止的位置)的高度h(cm)之间的函数关系式是
如图,弹簧挂着小球作上下振动,时间t(s)与小球相对平衡位置(即静止的位置)的高度h(cm)之间的函数关系式是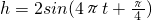 (t∈[0,+∞)),则小球最高点与最低点的距离、每秒能往复振动的次数分别为
(t∈[0,+∞)),则小球最高点与最低点的距离、每秒能往复振动的次数分别为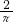
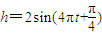 (t∈[0,+∞)),则小球最高点与最低点的距离、每秒能往复振动的次数分别为( )
(t∈[0,+∞)),则小球最高点与最低点的距离、每秒能往复振动的次数分别为( )


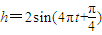 (t∈[0,+∞)),则小球最高点与最低点的距离、每秒能往复振动的次数分别为( )
(t∈[0,+∞)),则小球最高点与最低点的距离、每秒能往复振动的次数分别为( )


 (t∈[0,+∞)),则小球最高点与最低点的距离、每秒能往复振动的次数分别为( )
(t∈[0,+∞)),则小球最高点与最低点的距离、每秒能往复振动的次数分别为( )

