题目内容
有下列命题:①终边相同的角的同名三角函数的值相等;
②终边不同的角的同名三角函数的值不等;
③若sinα>0,则α是第一,二象限的角;
④若sinα=sinβ,则α=2kπ+β,k∈Z;
⑤已知α为第二象限的角,则
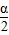 为第一象限的角.其中正确命题的序号有 .
为第一象限的角.其中正确命题的序号有 .
【答案】分析:根据三角函数的定义,终边相同的角所有的三角函数的值均相等;终边不同的角如果终边关于X轴对称,则余弦值相等,终边关于Y轴对称,则正弦值相等,终边关于原点对称,则正切值相等;若sinα>0,则α的终边落在第I、II象限或Y轴的非负半轴上;若sinα=sinβ,则α、β的终边重合或关于Y轴对称;若α为第二象限的角,则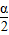 为第I、III象限的解,据此逐一对5个结论进行分析即可得到正确的答案.
为第I、III象限的解,据此逐一对5个结论进行分析即可得到正确的答案.
解答:解:三角函数的定义得,①正确;
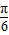 与-
与- 的终边不同,但cos
的终边不同,但cos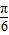 =cos(-
=cos(-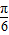 ),故②错误;
),故②错误;
若α=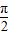 ,则sinα>0,但α不是第一,二象限的角,故③错误;
,则sinα>0,但α不是第一,二象限的角,故③错误;
令α=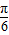 ,β=
,β=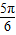 ,则sinα=sinβ,但α≠2kπ+β,k∈Z,故④错误;
,则sinα=sinβ,但α≠2kπ+β,k∈Z,故④错误;
α=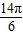 为第二象限的角,但
为第二象限的角,但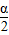 =
=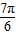 为第三象限的角,故⑤错误.
为第三象限的角,故⑤错误.
故答案为:①
点评:本题考查的知识点是利用终边相同的角的定义和性质,结合象限角与轴线角的定义,判断命题的真假,要判断一个命题为真命题,我们可以根据定义进行判断,若要判断一个命题为假命题,我们只要举出一个反例即可.
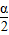 为第I、III象限的解,据此逐一对5个结论进行分析即可得到正确的答案.
为第I、III象限的解,据此逐一对5个结论进行分析即可得到正确的答案.解答:解:三角函数的定义得,①正确;
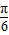 与-
与- 的终边不同,但cos
的终边不同,但cos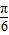 =cos(-
=cos(-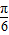 ),故②错误;
),故②错误;若α=
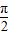 ,则sinα>0,但α不是第一,二象限的角,故③错误;
,则sinα>0,但α不是第一,二象限的角,故③错误;令α=
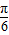 ,β=
,β=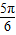 ,则sinα=sinβ,但α≠2kπ+β,k∈Z,故④错误;
,则sinα=sinβ,但α≠2kπ+β,k∈Z,故④错误;α=
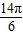 为第二象限的角,但
为第二象限的角,但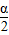 =
=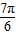 为第三象限的角,故⑤错误.
为第三象限的角,故⑤错误.故答案为:①
点评:本题考查的知识点是利用终边相同的角的定义和性质,结合象限角与轴线角的定义,判断命题的真假,要判断一个命题为真命题,我们可以根据定义进行判断,若要判断一个命题为假命题,我们只要举出一个反例即可.

练习册系列答案
相关题目
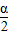 为第一象限的角.其中正确命题的序号有 .
为第一象限的角.其中正确命题的序号有 .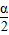 为第一象限的角.其中正确命题的序号有 .
为第一象限的角.其中正确命题的序号有 . 为第一象限的角.其中正确命题的序号有 .
为第一象限的角.其中正确命题的序号有 .