题目内容
把正整数排列成三角形数阵(如图甲),然后擦去第偶数行中的奇数和第奇数行中的偶数,得到新的三角形数阵(如图乙),再把图乙中的数按从小到大的顺序排成一列,得到一个数列{an},则a100=
【答案】分析:观察图乙中的事三角形数阵,发现第K(K是正整数)行最后一个数对应的序号是 ,然后解不等式100
,然后解不等式100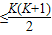 ,得到符合题意的最小整数K=14,由此可得a100应该在第14行.再观察数阵甲中与数阵乙中每行的首项数是相同的,不难由数阵甲得出第14行的第一个数,再转到数阵乙中找出a100即可.
,得到符合题意的最小整数K=14,由此可得a100应该在第14行.再观察数阵甲中与数阵乙中每行的首项数是相同的,不难由数阵甲得出第14行的第一个数,再转到数阵乙中找出a100即可.
解答:解:设图乙中第K行的最后一个数对应的序号为XK,不难由等差数列的求和公式得出
XK=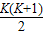 ,(K=1,2,3,…)
,(K=1,2,3,…)
解不等式100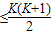 ,得最小正整数K=14,
,得最小正整数K=14,
说明a100在数阵乙的第14行,并且可以算得是第14行的第9个数
又因为数阵甲中与数阵乙中每行的首项数是相同的,在数阵甲中的每一行第一个数有如下规律:
2-1=1
5-2=3
10-5=5
…
b14-b13=2×13-1=25
累加,得b14-1=1+3+5+…+25=169,所以b14=170
数阵乙的第14行的第一个数也是170,往后数到第9项,按递增2的规律得:a100=170+2×8=186
故答案为:186
点评:本题以等差数列的三角形数阵为载体,考查了数列在实际生活中的应用,属于难题.观察对比两图形中的相同点与不同点,合理利用这此关系并结合等差数列的求和公式与通项公式,是解决本问题的关键.
 ,然后解不等式100
,然后解不等式100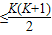 ,得到符合题意的最小整数K=14,由此可得a100应该在第14行.再观察数阵甲中与数阵乙中每行的首项数是相同的,不难由数阵甲得出第14行的第一个数,再转到数阵乙中找出a100即可.
,得到符合题意的最小整数K=14,由此可得a100应该在第14行.再观察数阵甲中与数阵乙中每行的首项数是相同的,不难由数阵甲得出第14行的第一个数,再转到数阵乙中找出a100即可.解答:解:设图乙中第K行的最后一个数对应的序号为XK,不难由等差数列的求和公式得出
XK=
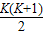 ,(K=1,2,3,…)
,(K=1,2,3,…)解不等式100
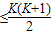 ,得最小正整数K=14,
,得最小正整数K=14,说明a100在数阵乙的第14行,并且可以算得是第14行的第9个数
又因为数阵甲中与数阵乙中每行的首项数是相同的,在数阵甲中的每一行第一个数有如下规律:
2-1=1
5-2=3
10-5=5
…
b14-b13=2×13-1=25
累加,得b14-1=1+3+5+…+25=169,所以b14=170
数阵乙的第14行的第一个数也是170,往后数到第9项,按递增2的规律得:a100=170+2×8=186
故答案为:186
点评:本题以等差数列的三角形数阵为载体,考查了数列在实际生活中的应用,属于难题.观察对比两图形中的相同点与不同点,合理利用这此关系并结合等差数列的求和公式与通项公式,是解决本问题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目



