题目内容
已知函数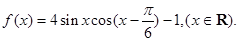
(I)求函数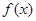 在区间
在区间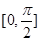 上的最大值和最小值;
上的最大值和最小值;
(Ⅱ)若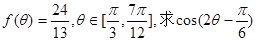 的值。
的值。
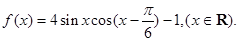
(I)求函数
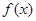 在区间
在区间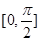 上的最大值和最小值;
上的最大值和最小值;(Ⅱ)若
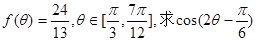 的值。
的值。(Ⅰ)函数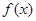 在区间
在区间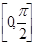 上的最大值为
上的最大值为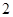 ,最小值为
,最小值为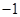 .(Ⅱ)
.(Ⅱ)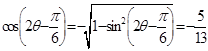 .
.
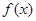 在区间
在区间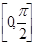 上的最大值为
上的最大值为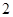 ,最小值为
,最小值为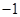 .(Ⅱ)
.(Ⅱ)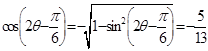 .
.(I)要借助三角恒等变换公式把f(x)转化成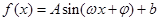 的形式是求解此类问题的基本思路。
的形式是求解此类问题的基本思路。
(II)根据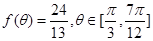 ,可求出
,可求出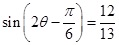 ,然后根据
,然后根据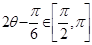 ,
,
可知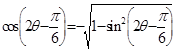
(Ⅰ)由题知:
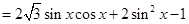 ,
,
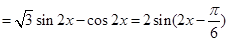 .……………………3分
.……………………3分
因为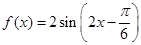 在区间
在区间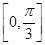 上为增函数,在区间
上为增函数,在区间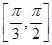 上为减函数
上为减函数
又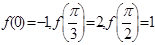 ,
,
所以函数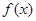 在区间
在区间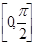 上的最大值为
上的最大值为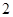 ,最小值为
,最小值为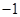 .……………………6分
.……………………6分
(Ⅱ)由(1)可知 ,又因为
,又因为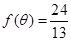 ,
,
所以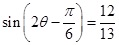 .………………9分
.………………9分
由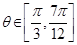 ,得
,得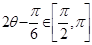 ,
,
从而,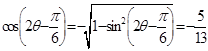 .
.
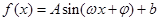 的形式是求解此类问题的基本思路。
的形式是求解此类问题的基本思路。(II)根据
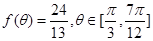 ,可求出
,可求出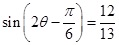 ,然后根据
,然后根据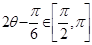 ,
,可知
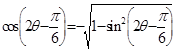
(Ⅰ)由题知:

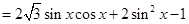 ,
, 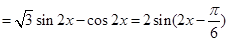 .……………………3分
.……………………3分因为
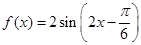 在区间
在区间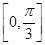 上为增函数,在区间
上为增函数,在区间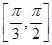 上为减函数
上为减函数 又
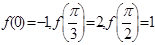 ,
,所以函数
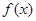 在区间
在区间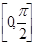 上的最大值为
上的最大值为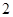 ,最小值为
,最小值为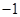 .……………………6分
.……………………6分(Ⅱ)由(1)可知
 ,又因为
,又因为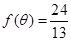 ,
,所以
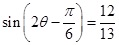 .………………9分
.………………9分由
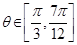 ,得
,得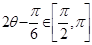 ,
,从而,
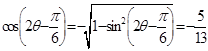 .
.
练习册系列答案
相关题目
 ,
, ,那么下列的点在角
,那么下列的点在角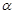 的终边上的是
的终边上的是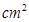 ,则扇形的圆心角的弧度数为( )
,则扇形的圆心角的弧度数为( )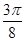 ,半径是1,则扇形的圆心角是
,半径是1,则扇形的圆心角是 

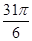 )的值.
)的值. 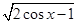 的定义域.
的定义域.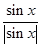 +
+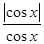 +
+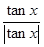 的值域.
的值域.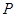
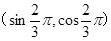 ,则角a的最小正角是( )
,则角a的最小正角是( )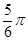
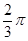
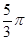
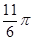
 .
.