题目内容
已知点A(cosα,sinα),点B(cos(α+
),sin(α+
)),点C(1,0).
(Ⅰ)若|CA|=
,求α的值;
(Ⅱ)若α∈(
,
),求
•
的取值范围.
| π |
| 3 |
| π |
| 3 |
(Ⅰ)若|CA|=
| 3 |
(Ⅱ)若α∈(
| π |
| 6 |
| π |
| 2 |
| CA |
| CB |
分析:(Ⅰ)由|CA|=
,可得 (cosα-1)2+sin2α=3,化简可得cosα=-
,由此求得 α 的值.
(Ⅱ)利用两个向量的数量积公式以及三角恒等变换化简
•
的解析式为
+
sin(α-
),由α∈(
,
),可得 α-
∈[-
,
],再根据正弦函数的定义域和值域求得
•
的取值范围.
| 3 |
| 1 |
| 2 |
(Ⅱ)利用两个向量的数量积公式以及三角恒等变换化简
| CA |
| CB |
| 1 |
| 2 |
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| CA |
| CB |
解答:解:(Ⅰ)若|CA|=
,则有 (cosα-1)2+sin2α=3,化简可得cosα=-
,∴α=2kπ+
,或α=2kπ+
,k∈z.
(Ⅱ)∵
•
=(cosα-1,sinα)•(cos(α+
)-1,sin(α+
))=(cosα-1)[cos(α+
)-1]+sinα•sin(α+
)
=(cosα-1)(
cosα-
sinα-1)+sinα(
sinα+
cosα)=
cos2α-
sinαcosα-cosα-
cosα+
sinα+1+
sin2α+
sinαcosα
=
-
cosα+
sinα=
+
(
sinα-
cosα)=
+
sin(α-
),
而由α∈(
,
),可得 α-
∈[-
,
],∴-
≤sin(α-
)≤
,∴-
≤
sin(α-
)≤
,
故
≤
•
≤
,即
•
的取值范围是[
,
].
| 3 |
| 1 |
| 2 |
| 2π |
| 3 |
| 4π |
| 3 |
(Ⅱ)∵
| CA |
| CB |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
=(cosα-1)(
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
=
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| π |
| 3 |
而由α∈(
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| π |
| 3 |
| ||
| 2 |
故
1-
| ||
| 2 |
| CA |
| CB |
1+
| ||
| 2 |
| CA |
| CB |
1-
| ||
| 2 |
1+
| ||
| 2 |
点评:本题主要考查两角和差的正弦公式,两个向量的数量积公式的应用,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
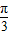 ),sin(α+
),sin(α+ )),点C(1,0).
)),点C(1,0).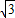 ,求α的值;
,求α的值; ),求
),求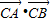 的取值范围.
的取值范围.