题目内容
当实数m分别取何值时，复数z=m2-3m-4+（m2+m）i为：
（1）虚数
（2）纯虚数
（3）对应点位于直线y=x上
（4）对应点在第二象限．
（1）虚数
（2）纯虚数
（3）对应点位于直线y=x上
（4）对应点在第二象限．
分析：（1）由虚部不等于0求得复数z为虚数的m的值；
（2）由实部等于0且虚部不等于0求得z为纯虚数的m的值；
（3）由实部和虚部相等求得z对应的点位于直线y=x上的m的值；
（4）由实部小于0且虚部大于0求解．
（2）由实部等于0且虚部不等于0求得z为纯虚数的m的值；
（3）由实部和虚部相等求得z对应的点位于直线y=x上的m的值；
（4）由实部小于0且虚部大于0求解．
解答：解：由m2-3m-4=0，得m=-1或m=4．
由m2+m=0，得m=0或m=-1．
（1）复数z=m2-3m-4+（m2+m）i为虚数，则m≠0，且m≠1；
（2）复数z=m2-3m-4+（m2+m）i为纯虚数，则m=4；
（3）复数z=m2-3m-4+（m2+m）i对应的点位于直线y=x上，
则m2-3m-4=m2+m，解得m=1；
（4）复数z=m2-3m-4+（m2+m）i对应点在第二象限
则
，解得0＜m＜4．
由m2+m=0，得m=0或m=-1．
（1）复数z=m2-3m-4+（m2+m）i为虚数，则m≠0，且m≠1；
（2）复数z=m2-3m-4+（m2+m）i为纯虚数，则m=4；
（3）复数z=m2-3m-4+（m2+m）i对应的点位于直线y=x上，
则m2-3m-4=m2+m，解得m=1；
（4）复数z=m2-3m-4+（m2+m）i对应点在第二象限
则
|
点评：本题考查了复数的基本概念，考查了复数的代数表示法及其几何意义，是基础的概念题．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
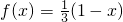且|f（a）|＜2，命题Q：集合A={x|x2+（a+2）x+1=0，x∈R}，B={x|x＞0}且A∩B=∅，
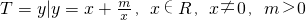，若?RT⊆S，求m的取值范围．