题目内容
选做题:请考生从22、23、24题中任选一题作答,并在答题卡上把所选题目的题号用2B铅笔涂黑.注意所做题目的题号必须与所涂的题号一致,在答题卡选答区域指定位置答题.如果多做,则按所做的第一题计分.如图,已知C、F是以AB为直径的半圆O上的两点,且CF=CB,过C作CD⊥AF交AF的延长线与点D.
(1)证明:CD为圆O的切线;
(2)若AD=3,AB=4,求AC的长.

【答案】分析:(Ⅰ)利用平行线的判定和性质定理、切线得出判定定理即可证明;
(Ⅱ)利用相似三角形的性质定理即可求出.
解答: (Ⅰ)证明:∵CF=CB,∴∠CAF=∠CAB.
(Ⅰ)证明:∵CF=CB,∴∠CAF=∠CAB.
∵OA=OC,∴∠CAO=∠ACO,
∴∠CAF=∠ACO,∴AF∥OC.
∵CD⊥AF,∴CD⊥OC.
∴CD为圆O的切线.
(Ⅱ)解:连接BC,由(Ⅰ)知∠CAD=∠CAB.
又∠CDA=∠ACB=90°,∴△ADC∽△ACB.
∴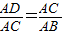 .
.
∴AC2=AD•AB=12,∴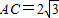 .
.
点评:熟练掌握平行线的判定和性质定理、切线得出判定定理、相似三角形的性质定理是解题的关键.
(Ⅱ)利用相似三角形的性质定理即可求出.
解答:
 (Ⅰ)证明:∵CF=CB,∴∠CAF=∠CAB.
(Ⅰ)证明:∵CF=CB,∴∠CAF=∠CAB.∵OA=OC,∴∠CAO=∠ACO,
∴∠CAF=∠ACO,∴AF∥OC.
∵CD⊥AF,∴CD⊥OC.
∴CD为圆O的切线.
(Ⅱ)解:连接BC,由(Ⅰ)知∠CAD=∠CAB.
又∠CDA=∠ACB=90°,∴△ADC∽△ACB.
∴
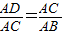 .
.∴AC2=AD•AB=12,∴
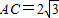 .
.点评:熟练掌握平行线的判定和性质定理、切线得出判定定理、相似三角形的性质定理是解题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
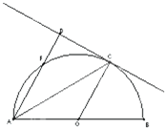 选做题:请考生从22、23、24题中任选一题作答,并在答题卡上把所选题目的题号用2B铅笔涂黑.注意所做题目的题号必须与所涂的题号一致,在答题卡选答区域指定位置答题.如果多做,则按所做的第一题计分.
选做题:请考生从22、23、24题中任选一题作答,并在答题卡上把所选题目的题号用2B铅笔涂黑.注意所做题目的题号必须与所涂的题号一致,在答题卡选答区域指定位置答题.如果多做,则按所做的第一题计分. 选做题:请考生从22、23、24题中任选一题作答,并在答题卡上把所选题目的题号用2B铅笔涂黑.注意所做题目的题号必须与所涂的题号一致,在答题卡选答区域指定位置答题.如果多做,则按所做的第一题计分.
选做题:请考生从22、23、24题中任选一题作答,并在答题卡上把所选题目的题号用2B铅笔涂黑.注意所做题目的题号必须与所涂的题号一致,在答题卡选答区域指定位置答题.如果多做,则按所做的第一题计分.