题目内容
曲线C：（5-m）x2+（m-2）y2=8（m∈R）表示焦点在x轴上的椭圆，则m取值范围________．
＜m＜5分析：将椭圆C的方程标准化，利用其焦点在x轴上即可求得答案．
解答：∵（5-m）x2+（m-2）y2=8（m∈R）表示焦点在x轴上的椭圆，
∴
+
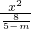=1表示焦点在x轴上的椭圆，∴
＞
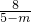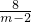＞0，解得：
＜m＜5．∴m的取值范围是：
＜m＜5．故答案为：
＜m＜5．点评：本题考查椭圆的标准方程，考查椭圆的性质与解不等式组的能力，属于中档题．
练习册系列答案
相关题目
，求m的取值范围；