题目内容
函数
的图像恒过定点A，若点A在直线
上，其中mn>0，则
的最小值为（ ）
的图像恒过定点A，若点A在直线上，其中mn>0，则的最小值为（ ）| A．1 | B．2 | C．3 | D．4 |
B
试题分析：由题意可得函数
的图像恒过定点A（1，1），又点A在直线mx+ny-2=0=0上，∴m+n=2，∴
=
，当且仅当
，时取“=”可得m=n=1，所以的最小值为2，故选B点评：基本不等式是求解二元最值问题的常用方法，本题用到了“1”的代换及函数图象过定点问题，解题过程中用到了转化的思想，是一道基础题
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
若
的最大值为8，则k=_____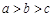
且
恒成立，则k的最大值是（ ）
则
的最小值为（ ）
在由不等式组
确定的平面区域内，则点
所在平面区域的面积是 。
，若
，
，则
的最大值为（ ）
为正数，且
．求
的最小值.