题目内容
设函数f（x）＝a（x＋
）＋2lnx，g（x）＝
．
（Ⅰ）若a>0且a≠2，直线l与函数f（x）和函数g（x）的图象相切于一点，求切线l的方程．
（Ⅱ）若f（x）在[2，4]内为单调函数，求实数a的取值范围；
解：（Ⅰ）∵
=
，∴
因为直线
与函数
的图象相切于同一点
……………………………………………………………4分
解得
(
)，（
舍去）
,
;
,
,
;
,
①当
时，则的方程为:
②当
时，又因为点（
也在
有
即
令
，
易得方程在
一定有解
所以的方程为
综上所述直线的方程为或………………6分
（Ⅱ）∵=
要使在[2,4]为单调增函数，须
在[2,4]恒成立，
即
在[2,4]恒成立，即
在[2,4]恒成立，
又
即
(
) ……………………8分
设
(),因为
(
)所以
在
)上单调递减.
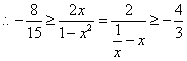
所以当
时，在[2,4]为单调增函数；………………………………10分
同理要使为单调减函数，须
在[2,4]恒成立，
易得
综上，若在[2,4]为单调函数，则
的取值范围为或…12分
练习册系列答案
阳光课堂课时作业系列答案
相关题目
，sin
－sin（2x－
）．
）＝
，若sinB＝2sinA，求△ABC的面积．
－lnx，则y＝f（x）
，1），（1，e）内均有零点
（a>0），且f（2）＝4，则