题目内容
如图,B地在A地的正东方向4 km处,C地在B地的北
偏东30°方向2 km处,河流的沿岸PQ(曲线)上任意一点
到A的距离比到B的距离远2 km..现要在曲线PQ上选一处
M建一座码头,向B、C两地转运货物.那么这两条公路MB、
MC的路程之和最短是 km

偏东30°方向2 km处,河流的沿岸PQ(曲线)上任意一点
到A的距离比到B的距离远2 km..现要在曲线PQ上选一处
M建一座码头,向B、C两地转运货物.那么这两条公路MB、
MC的路程之和最短是 km



如图,将A,B放入直角坐标系中。由河岸上任意一点到A的距离比到B的距离远2KM。知河岸为双曲线的一支。为了方便,设
 所在的直线为
所在的直线为 轴,它们的中点为原点。
轴,它们的中点为原点。
则可得到
 .
. 在
在 北偏东
北偏东 ,则
,则 .
.设
 ,则设
,则设 ①,且
①,且 ②.
②.所以当①最小时,上面两式联立,得,
 为最小,此时
为最小,此时 在同一条直线上。
在同一条直线上。此时
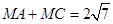 。所以 有
。所以 有 的最小值为
的最小值为
本题可以根据双曲线的定义来解题,为简化计算可以利用A点。如果求出双曲线的方程,计算将非常繁琐。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 中,设角A、B、C的对边为a、b、c,且
中,设角A、B、C的对边为a、b、c,且 ( )
( ) 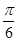 B.
B.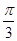 C.
C. D.
D.
 中,
中, 所对的边分别是
所对的边分别是 ,若
,若 ▲ .
▲ . 题满分13分)
题满分13分) 在△ABC中,角A、B、C所对的边分别为a、b、c,且CosA=
在△ABC中,角A、B、C所对的边分别为a、b、c,且CosA= ,向量 =
,向量 = ,
,
 ,且 ⊥
,且 ⊥  中,若
中,若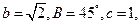 则
则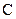 =___________.
=___________. 中,若
中,若 ,则
,则