题目内容
已知命题:“ ,使等式
,使等式 成立”是真命题.
成立”是真命题.
(1)求实数m的取值集合M;
(2)设不等式 的解集为N,若
的解集为N,若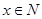 是
是 的必要条件,求a的取值范围.
的必要条件,求a的取值范围.
【答案】
(1)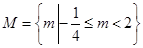 ;(2)
;(2)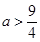 或
或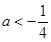 .
.
【解析】
试题分析:(1)本题是一个一元二次方程在某个区间上有解的问题,通常有两种方法,一是考察相应的二次函数的图象零点的分布,二是分离参数转化为求函数的值域问题,由于本题较容易分离参数,所以采用第二种方法,化为求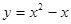 在
在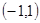 上的值域;(2)根据
上的值域;(2)根据 是
是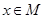 的必要条件得
的必要条件得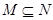 ,
,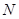 就是一个一元二次不等式的解集,在求解时要讨论相应一元二次方程两根的大小,写出解集后,再由
就是一个一元二次不等式的解集,在求解时要讨论相应一元二次方程两根的大小,写出解集后,再由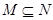 ,通过使用数轴求出
,通过使用数轴求出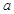 的取值范围.
的取值范围.
试题解析:(1) 由题意知,方程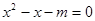 在
在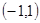 上有解,
上有解,
即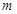 的取值范围就为函数
的取值范围就为函数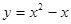 在
在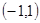 上的值域,易得
上的值域,易得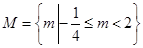
(2)因为 是
是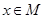 的必要条件,所以
的必要条件,所以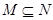
当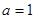 时,解集
时,解集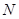 为空集,不满足题意
为空集,不满足题意
当 时,
时,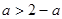 ,此时集合
,此时集合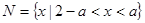
则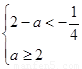 ,解得
,解得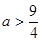
当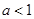 时,
时,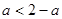 ,此时集合
,此时集合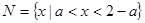
则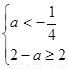 ,解得
,解得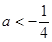
综上,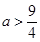 或
或
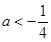
考点:函数与方程、充分条件与必要条件、集合的包含关系,一元二次不等式.

练习册系列答案
相关题目