题目内容
已知函数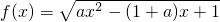
(1)当a=0时,求证函数f(x)在它的定义域上单调递减
(2)是否存在实数a使得区间[-1,1]上一切x都满足f(x)≤ ,若存在,求实数a的值;若不存在,说明理由.
,若存在,求实数a的值;若不存在,说明理由.
解:(1)a=0时, ,定义域为(-∞,1];
,定义域为(-∞,1];
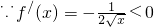
∴函数f(x)在它的定义域上单调递减
(2)假设存在实数a使得区间[-1,1]上一切x都满足f(x)≤ ,
,
即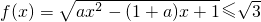
即-1≤ax2-(1+a)x≤2在区间[-1,1]上恒成立
∴-1≤2a+1≤2
∴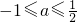
分析:(1)当a=0时,利用被开方数大于等于0 可求函数的定义域,利用导数小于0,可证在它的定义域上单调递减
(2)假设存在实数a使得区间[-1,1]上一切x都满足f(x)≤ ,两边平方即可求得.
,两边平方即可求得.
点评:本题以函数为载体,考查函数的单调性,考查存在性问题,关键是等价转化.
 ,定义域为(-∞,1];
,定义域为(-∞,1];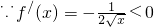
∴函数f(x)在它的定义域上单调递减
(2)假设存在实数a使得区间[-1,1]上一切x都满足f(x)≤
 ,
,即
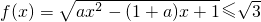
即-1≤ax2-(1+a)x≤2在区间[-1,1]上恒成立
∴-1≤2a+1≤2
∴
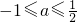
分析:(1)当a=0时,利用被开方数大于等于0 可求函数的定义域,利用导数小于0,可证在它的定义域上单调递减
(2)假设存在实数a使得区间[-1,1]上一切x都满足f(x)≤
 ,两边平方即可求得.
,两边平方即可求得.点评:本题以函数为载体,考查函数的单调性,考查存在性问题,关键是等价转化.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
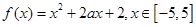
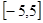 上是单调函数
上是单调函数 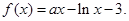
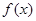 在点(1,-2)处的切线方程;
在点(1,-2)处的切线方程;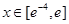 上的图象与直线
上的图象与直线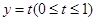 总有两个不同交点,求实数a的取值范围。
总有两个不同交点,求实数a的取值范围。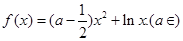
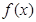 在区间[1,e]上的最大值和最小值;
在区间[1,e]上的最大值和最小值;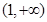 上,函数
上,函数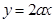 下方,求a的取值范围。
下方,求a的取值范围。
 的图象与直线y=ax只有一个公共点,求实数b的取值范围。
的图象与直线y=ax只有一个公共点,求实数b的取值范围。
 的图象与直线y=ax只有一个公共点,求实数b的取值范围。
的图象与直线y=ax只有一个公共点,求实数b的取值范围。