题目内容
设A,B,C,D是空间四个不同的点,在下列命题中,不正确的是( )A.若AC与BD共面,则AD与BC共面
B.若AC与BD是异面直线,则AD与BC是异面直线
C.若AB=AC,DB=DC,则AD=BC
D.若AC=AC,DB=DC,则AD⊥BC
思路解析:易证A正确;对B,若AD与BC不是异面直线,则AD与BC共面,从而AC与BD共面,这与已知条件AC与BD是异面直线矛盾,所以AD与BC是异面直线;对于C,如图2-1-16所示,虽然AB=AC,DB=DC,但BC与AD的长可大可小,所以没有什么关系;对于D,取BC的中点O,连结AO,DO,
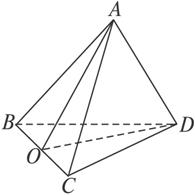
图2-1-16
∵AB=AC,∴AO⊥BC.
又∵DB=DC,
∴DO⊥BC.
∴BC⊥平面AOD.
∴BC⊥AD.
答案:C

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
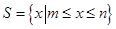 满足:当
满足:当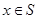 时,有
时,有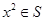 ,给出如下三个命题:
,给出如下三个命题: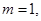 则
则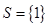 ;②若
;②若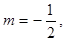 则
则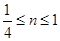 ; ③若
; ③若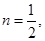 则
则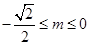 .
.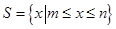 满足:当
满足:当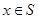 时,有
时,有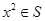 ,给出如下三个命题:
,给出如下三个命题: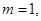 则
则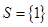 ;②若
;②若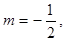 则
则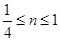 ; ③若
; ③若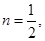 则
则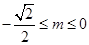 .
.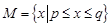 满足:当
满足:当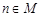 时,有
时,有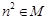 .现
.现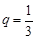 ,则
,则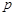 的范围是(▲)
的范围是(▲)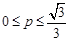 B.
B.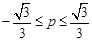 C.
C.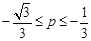 D.
D.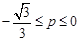
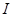 为全集,
为全集,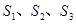 是
是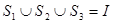 ,则下面论断正确的是 (
)
,则下面论断正确的是 (
) B
B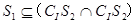
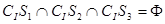 D
D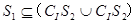 .
.