题目内容
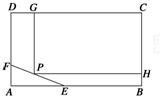为了保护环境，实现城市绿化，某房地产公司要在拆迁地长方形ABCD上规划出一块长方形地面建造公园，公园一边落在CD上，但不得越过文物保护区△AEF的EF．问如何设才能使公园占地面积最大，并求这最大面积（其中AB=200 m，BC=160m，AE=60m，AF=40m．）
分析：设CG=x，矩形CGPH面积为y，作EN⊥PH于点N，因为三角形AEF∽三角形PEN，得到对应边成比例得到EN，用160-EN得到HC，然后利用矩形的面积求法，长乘以宽得到y与x的函数关系式，最后利用基本不等式求出最大值即可．
解答：
解：设CG=x，矩形CGPH面积为y，
作EN⊥PH于点N，则
=
?EN=
∴HC=160-
=
y=x•
=
•2x（760-2x）≤
（(
)2=
当2x=760-2x?x=190（m）即CG长为190m时，最大面积为
（m2）
答：当CG长为190m时，公园占地面积最大，最大面积为
（m2）
解：设CG=x，矩形CGPH面积为y，作EN⊥PH于点N，则
| EN |
| 40 |
| x-140 |
| 60 |
| 2x-280 |
| 3 |
∴HC=160-
| 2x-280 |
| 3 |
| 760-2x |
| 3 |
y=x•
| 760-2x |
| 3 |
| 1 |
| 6 |
| 1 |
| 6 |
| 760 |
| 2 |
| 72200 |
| 3 |
当2x=760-2x?x=190（m）即CG长为190m时，最大面积为
| 72200 |
| 3 |
答：当CG长为190m时，公园占地面积最大，最大面积为
| 72200 |
| 3 |
点评：考查学生会根据实际问题选择合适的函数类型来解决实际问题，理解函数的最值及其几何意义．
练习册系列答案
相关题目
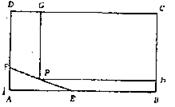
上规划出一块长方形地面建造公园，公园一边落在CD上，但不得越过文物保护区
的EF.问如何设计才能使公园占地面积最大，并求这最大面积.（ 其中AB=200m，BC=160m，AE=60m，AF=40m.）
上规划出一块长方形地面建造公园，公园一边落在CD 上，但不得越过文物保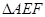
的EF.问如何设才能使公园占地面积最大，并求这最大面积（ 其中AB=200 
