题目内容
如图,若平面α⊥β,α∩β=CD,A∈α、B∈β,直线AB与α、β所成的角分别是30°、60°,则直线AB与CD所成角的大小为( )
分析:如果空间想象能力较强,注意到30°、60°、90°三角的关系,可以果断判断AB与CD垂直,如果按常规作法,需要先作出线AB与CD所成角的平面角,再计算,在这个过程中发现只有当AB与CD垂直时才能得结果,从而作出判断
解答:解:如图作BF⊥CD,AE⊥CD,AG∥EF,AG=EF,连接BE,FG,AF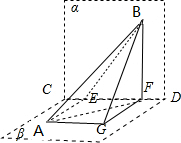
∵平面α⊥β,∴AE⊥α,BF⊥β
∵直线AB与α、β所成的角分别是30°、60°
∴∠ABE=30°,∠BAF=60°,
设AB=2,则AE=1,AF=1,
∵△AEF为直角三角形,
∴E、F两点重合
∴CD⊥平面ABE(F),AB?平面ABE(F),
∴CD⊥AB
即线AB与CD所成角的大小为90°
故选D

∵平面α⊥β,∴AE⊥α,BF⊥β
∵直线AB与α、β所成的角分别是30°、60°
∴∠ABE=30°,∠BAF=60°,
设AB=2,则AE=1,AF=1,
∵△AEF为直角三角形,
∴E、F两点重合
∴CD⊥平面ABE(F),AB?平面ABE(F),
∴CD⊥AB
即线AB与CD所成角的大小为90°
故选D
点评:本题考察了空间想象能力,空间线面角的作法,面面垂直的性质定理等知识,考查了同一性的思想,判断推理的能力

练习册系列答案
相关题目