题目内容
考察等式:
+
+…+
=
(*),其中n、m、r∈N*,r≤m<n且r≤n-m.某同学用概率论方法证明等式(*)如下:
设一批产品共有n件,其中m件是次品,其余为正品.现从中随机取出r件产品,
记事件Ak={取到的r件产品中恰有k件次品},则P(Ak)=
,k=0,1,2,…,r.
显然A0,A1,…,Ar为互斥事件,且A0∪A1∪…∪Ar=Ω(必然事件),
因此1=P(Ω)=P(A0)+P(A1)+…P(Ar)=
,
所以
+
+…+
=
,即等式(*)成立.
对此,有的同学认为上述证明是正确的,体现了偶然性与必然性的统一;但有的同学对上述证明方法的科学性与严谨性提出质疑.现有以下四个判断:
①等式(*)成立 ②等式(*)不成立 ③证明正确 ④证明不正确
试写出所有正确判断的序号______.
| C | 0m |
| C | rn-m |
| C | 1m |
| C | r-1n-m |
| C | rm |
| C | 0n-m |
| C | rn |
设一批产品共有n件,其中m件是次品,其余为正品.现从中随机取出r件产品,
记事件Ak={取到的r件产品中恰有k件次品},则P(Ak)=
| ||||
|
显然A0,A1,…,Ar为互斥事件,且A0∪A1∪…∪Ar=Ω(必然事件),
因此1=P(Ω)=P(A0)+P(A1)+…P(Ar)=
| ||||||||||||
|
所以
| C | 0m |
| C | rn-m |
| C | 1m |
| C | r-1n-m |
| C | rm |
| C | 0n-m |
| C | rn |
对此,有的同学认为上述证明是正确的,体现了偶然性与必然性的统一;但有的同学对上述证明方法的科学性与严谨性提出质疑.现有以下四个判断:
①等式(*)成立 ②等式(*)不成立 ③证明正确 ④证明不正确
试写出所有正确判断的序号______.
设一批产品共有n件,其中m件是次品,其余n-m件为正品.
现从中随机取出r件产品,记事件Ak={取到的产品中恰有k件次品},则取到的产品中恰有k件次品共有
种情况,又从中随机取出r件产品,共有
种情况,k=0,1,…,r,故其概率为P(Ak)=
,k=0,1,…,r.
∵A0,A1,…,Ar为互斥事件,且A0∪A1∪…∪Ar=Ω(必然事件),
因此1=P(Ω)=P(A0)+P(A1)+…P(Ar)=
,
所以Cm0Cn-mr+Cm1Cn-mr-1+…+CmrCn-m0=Cnr,即等式(*)成立.
从而可知正确的序号为:①③
故答案为:①③
现从中随机取出r件产品,记事件Ak={取到的产品中恰有k件次品},则取到的产品中恰有k件次品共有
| C | km |
| C | r-kn-m |
| C | rn |
| ||||
|
∵A0,A1,…,Ar为互斥事件,且A0∪A1∪…∪Ar=Ω(必然事件),
因此1=P(Ω)=P(A0)+P(A1)+…P(Ar)=
| ||||||||||||
|
所以Cm0Cn-mr+Cm1Cn-mr-1+…+CmrCn-m0=Cnr,即等式(*)成立.
从而可知正确的序号为:①③
故答案为:①③

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
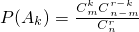 ,k=0,1,…,r.显然A0,A1,…,Ar为互斥事件,且A0∪A1∪…∪Ar=Ω(必然事件),因此1=P(Ω)=P(A0)+P(A1)+…P(Ar)=
,k=0,1,…,r.显然A0,A1,…,Ar为互斥事件,且A0∪A1∪…∪Ar=Ω(必然事件),因此1=P(Ω)=P(A0)+P(A1)+…P(Ar)=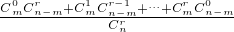 ,所以Cm0Cn-mr+Cm1Cn-mr-1+…+CmrCn-m0=Cnr,即等式(*)成立.对此,有的同学认为上述证明是正确的,体现了偶然性与必然性的统一;但有的同学对上述证明方法的科学性与严谨性提出质疑.现有以下四个判断:
,所以Cm0Cn-mr+Cm1Cn-mr-1+…+CmrCn-m0=Cnr,即等式(*)成立.对此,有的同学认为上述证明是正确的,体现了偶然性与必然性的统一;但有的同学对上述证明方法的科学性与严谨性提出质疑.现有以下四个判断: (*),其中n、m、r∈N*,r≤m<n且r≤n-m.某同学用概率论方法证明等式(*)如下:
(*),其中n、m、r∈N*,r≤m<n且r≤n-m.某同学用概率论方法证明等式(*)如下: ,k=0,1,2,…,r.
,k=0,1,2,…,r. ,
, ,即等式(*)成立.
,即等式(*)成立. (*)
(*) ,k=0,1,…,r。显然A0,A1,…,Ar为互斥事件,且
,k=0,1,…,r。显然A0,A1,…,Ar为互斥事件,且 (必然事件),因此
(必然事件),因此
 ,
, ,即等式(*)成立。
,即等式(*)成立。