题目内容
已知 ;
;
(1)求证: ;(2)求证:
;(2)求证: .
.
 ;
;(1)求证:
 ;(2)求证:
;(2)求证: .
.(1)利用两角和差公式化简求证即可(2)化弦为切即可证明
试题分析:(1)∵
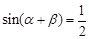 ,,∴
,,∴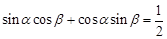 ……①
……①∵
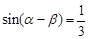 ,∴
,∴ ……②
……②联立①②解得
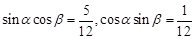 ,∴
,∴ ,得证
,得证(2)由
 得
得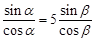 ,∴
,∴ ,得证
,得证点评:三角求值题解题的一般思路是“变角、变名、变式” ,变角:它决定变换的方向,通过找出已知条件和待求结论中的差异,分析角之间的联系,决定用哪一组公式,是解决问题的关键;变名:在同一个三角式中尽可能使三角函数的种类最少,一般考虑化弦或化切(用同角三角函数的关系式或万能公式);变式:由前二步对三角式进行恒等变形,或逆用、变形用公式,使问题获解;

练习册系列答案
相关题目
 ,且
,且 ,
, 的值;
的值; 的值.
的值. ( )
( )

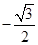

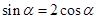 ,那么
,那么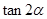 的值为 .
的值为 .
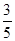 ,tan
,tan =
= ,那么tan(α+
,那么tan(α+ )的值为 .
)的值为 .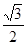
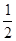
 ,则
,则 的值为( )
的值为( )

