题目内容
下图是函数f(x)=Asinωx(A>0,ω>0)一个周期的图象,则f(1)+f(2)+f(3)+f(4)+f(5)+f(6)的值等于( )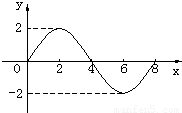
A.
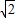
B.
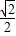
C.
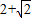
D.
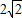
【答案】分析:由函数f(x)的图象得到函数的最大值为2,即为A的值,再根据图象可得函数的周期为8,利用周期公式即可求出ω的值,从而确定出函数的解析式,然后把x=1,2,3,4,5,6分别代入函数解析式中,利用特殊角的三角函数值即可求出所求式子的值.
解答:解:由函数f(x)的图象可知:f(x)解析式中A=2,
且函数f(x)的周期为8,则有T=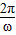 =8,解得ω=
=8,解得ω=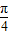 ,
,
所以函数f(x)=2sin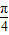 x,
x,
则f(1)+f(2)+f(3)+f(4)+f(5)+f(6)
=2sin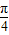 +2sin
+2sin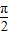 +2sin
+2sin +2sinπ+2sin
+2sinπ+2sin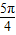 +2sin
+2sin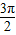
=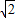 +2+
+2+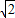 +0-
+0-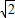 -2
-2
=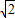 .
.
故选A
点评:此题考查了由y=Asin(ωx+φ)的部分图象确定其解析式,考查了数形结合的思想,借助图形找出函数的周期及函数的最值是解本题的关键.
解答:解:由函数f(x)的图象可知:f(x)解析式中A=2,
且函数f(x)的周期为8,则有T=
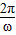 =8,解得ω=
=8,解得ω=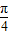 ,
,所以函数f(x)=2sin
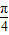 x,
x,则f(1)+f(2)+f(3)+f(4)+f(5)+f(6)
=2sin
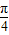 +2sin
+2sin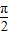 +2sin
+2sin +2sinπ+2sin
+2sinπ+2sin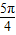 +2sin
+2sin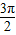
=
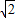 +2+
+2+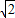 +0-
+0-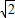 -2
-2=
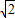 .
.故选A
点评:此题考查了由y=Asin(ωx+φ)的部分图象确定其解析式,考查了数形结合的思想,借助图形找出函数的周期及函数的最值是解本题的关键.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
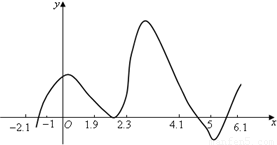
 6、下图是函数f(x)的图象,它与x轴有4个不同的公共点.给出下列四个区间之中,存在不能用二分法求出的零点,该零点所在的区间是( )
6、下图是函数f(x)的图象,它与x轴有4个不同的公共点.给出下列四个区间之中,存在不能用二分法求出的零点,该零点所在的区间是( )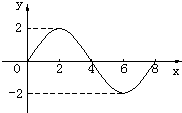
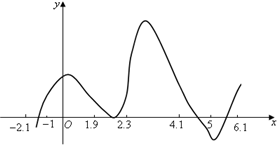 5、下图是函数f(x)的图象,它与x轴有4个不同的公共点.给出下列四个区间,不能用二分法求出函数f(x)在区间( ) 上的零点的是( )
5、下图是函数f(x)的图象,它与x轴有4个不同的公共点.给出下列四个区间,不能用二分法求出函数f(x)在区间( ) 上的零点的是( )