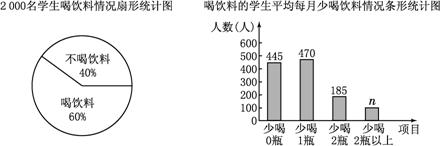
题目内容
某校课外兴趣小组的学生为了给学校边的一口被污染的池塘治污,他们通过实验后决定在池塘中投放一种能与水中的污染物质发生化学反应的药剂.已知每投放 个单位的药剂,它在水中释放的浓度
个单位的药剂,它在水中释放的浓度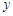 (克/升)随着时间
(克/升)随着时间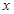 (天)变化的函数关系式近似为
(天)变化的函数关系式近似为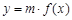 ,其中
,其中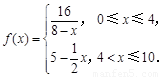 若多次投放,则某一时刻水中的药剂浓度为各次投放的药剂在相应时刻所释放的浓度之和.根据经验,当水中药剂的浓度不低于4(克/升)时,它才能起到有效治污的作用.
若多次投放,则某一时刻水中的药剂浓度为各次投放的药剂在相应时刻所释放的浓度之和.根据经验,当水中药剂的浓度不低于4(克/升)时,它才能起到有效治污的作用.
(Ⅰ)若一次投放4个单位的药剂,则有效治污时间可达几天?
(Ⅱ)若第一次投放2个单位的药剂,6天后再投放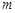 个单位的药剂,要使接下来的4天中能够持续有效治污,试求
个单位的药剂,要使接下来的4天中能够持续有效治污,试求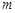 的最小值.
的最小值.
【答案】
(Ⅰ)有效治污的时间可达8天; (Ⅱ)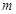 的最小值为1
的最小值为1
【解析】
试题分析:(Ⅰ)先由 可得在水中释放的浓度
可得在水中释放的浓度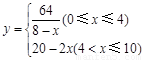 再分别分段求出水中药剂的浓度不低于4(克/升)时的天数,从而得出有效治污的时间可达8天;
再分别分段求出水中药剂的浓度不低于4(克/升)时的天数,从而得出有效治污的时间可达8天;
(Ⅱ)先得出模型当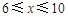 时,
时, ,然后由基本不等式知
,然后由基本不等式知 ,再由
,再由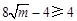 ,解得
,解得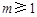 ,即
,即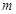 的最小值为1 .
的最小值为1 .
试题解析:(I)∵ ∴
∴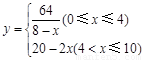 .
2分
.
2分
当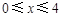 时,由
时,由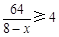 ,解得
,解得 ,此时
,此时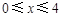 ;
;
当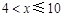 时,由
时,由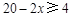 ,解得
,解得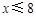 ,此时
,此时 . 4分
. 4分
综上,得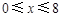 .故若一次投放4个单位的药剂,则有效治污的时间可达8天.6分
.故若一次投放4个单位的药剂,则有效治污的时间可达8天.6分
(II)当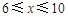 时,
时, ,9分
,9分
又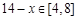 ,
, 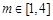 ,则
,则 .
.
当且仅当 ,即
,即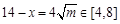 时取等号.
时取等号.
令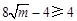 ,解得
,解得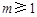 ,故所求
,故所求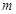 的最小值为1 .
14分
的最小值为1 .
14分
考点:1.函数模型的应用;2.基本不等式的应用

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目